
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Деление направленного отрезка в данном отношении
|
|
|
|
Пусть на одной и той же прямой лежат два направленных отрезка 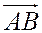 и
и 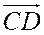 , причем
, причем 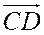 невырожденный направленный отрезок. Тогда отношение
невырожденный направленный отрезок. Тогда отношение  в случае, если направленный отрезок
в случае, если направленный отрезок 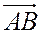 также невырожденный, называется число
также невырожденный, называется число  , абсолютная величина которого равна
, абсолютная величина которого равна  и которое положительно, если
и которое положительно, если 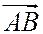 и
и  имеют одинаковое направление, и отрицательно в противном случае. Если отрезок
имеют одинаковое направление, и отрицательно в противном случае. Если отрезок 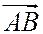 вырожденный, а отрезок
вырожденный, а отрезок  невырожденный, то будем считать, что
невырожденный, то будем считать, что 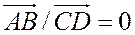 . Если отрезок
. Если отрезок 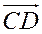 вырожденный, то отношение
вырожденный, то отношение  не определяется.
не определяется.
Если отношение 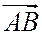 к
к  равно
равно  , то пишут
, то пишут  .
.
Пусть на некоторой прямой задан невырожденный направленный отрезок  и путь С – какая-нибудь точка этой прямой, отличная от точки В.
и путь С – какая-нибудь точка этой прямой, отличная от точки В.
Отношением, в котором точка С делит невырожденный направленный отрезок 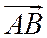 , называется число
, называется число  , определяемое соотношением
, определяемое соотношением  .
.
Из этого определения следует, что 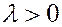 , если точка С лежит между
, если точка С лежит между
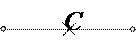
А В точками А и В, и  в противном случае.
в противном случае.
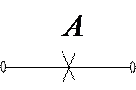 При этом
При этом 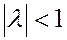 , если точка А лежит между
, если точка А лежит между
точками В и С.
B C
И  , если точка В лежит между точками А и С.
, если точка В лежит между точками А и С.
 |
А С
Заметим, что отношение, в котором точка С делит невырожденный направленный отрезок 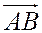 , никогда не равно -1.
, никогда не равно -1.
Теорема 4. Если на оси координат заданы две различные точки 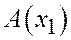 и
и  и, если точка
и, если точка  делит направленный отрезок
делит направленный отрезок 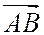 в отношении
в отношении  , то
, то
 ; и
; и 
Доказательство. Из данного определения отношения  , в котором точка С делит невырожденный направленный отрезок
, в котором точка С делит невырожденный направленный отрезок 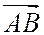 , а также из определения координаты направленного отрезка, лежащего на оси, следует
, а также из определения координаты направленного отрезка, лежащего на оси, следует
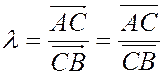
значит на основании теоремы 2 § 4 (то,что координата 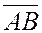 направленного отрезка
направленного отрезка 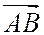 заданного двумя точками
заданного двумя точками  и
и  оси координат, вычисляются по формуле
оси координат, вычисляются по формуле  ), имеем:
), имеем:  , откуда
, откуда  .
.
Следствие. Координата середины отрезка равна полусумме координат его концов: 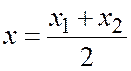 . В самом деле: для середины отрезка
. В самом деле: для середины отрезка  .
.
Определение. Простым отношением (АВС) трех точек А, В, С лежащих на одной прямой и взятых в определенном порядке (А, В, С) называется число  , равное
, равное
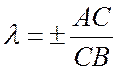 ,
,
причем перед дробью ставится знак «+», если точка С лежит между А и В, и знак «-» в противном случае.
Определение. Сложным, или ангармоническим, отношением четырех точек А, В, С, D, лежащих на одной прямой (точки А и В различны, С и D различны), называется число
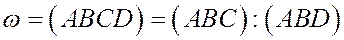
Если  =-1, то говорят, что точка С и D гармонически разделены точками А и В.
=-1, то говорят, что точка С и D гармонически разделены точками А и В.
Теорема 5. Каково бы ни было число 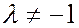 , существует и притом только одна точка С, которая делит невырожденный направленный отрезок
, существует и притом только одна точка С, которая делит невырожденный направленный отрезок 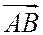 в отношении
в отношении 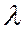 .
.
Доказательство. Введем на прямой АВ систему координат. Предполагая, что некоторая точка С (х) делит направленный отрезок 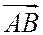 в отношении
в отношении  , на основании предыдущей теоремы найдем
, на основании предыдущей теоремы найдем
 ,
,
где  и
и  - координаты точек А и В. Этим доказана единственность точки С, делящей направленный отрезок
- координаты точек А и В. Этим доказана единственность точки С, делящей направленный отрезок 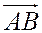 в данном отношении
в данном отношении  , т.е. доказано, что если такая точка существует, то только одна.
, т.е. доказано, что если такая точка существует, то только одна.
Далее, точка С с координатой
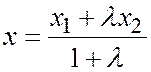
делит направленный отрезок  в отношении
в отношении 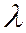 , так как из написанного соотношения следует
, так как из написанного соотношения следует

Точки С и В различны, так как разность их координат не равна нулю; в самом деле,
 (т.к.
(т.к. 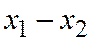 это
это  но
но 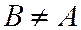 поскольку по условию теоремы отрезок
поскольку по условию теоремы отрезок 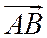 невырожденный).
невырожденный).
Поэтому  и из последнего равенства следует, что
и из последнего равенства следует, что
 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 974; Нарушение авторских прав?; Мы поможем в написании вашей работы!