Идеального газа по скоростям и энергиям

Закон Максвелла распределения молекул

Среднее число столкновений и средняя длина свободного пробега молекул.

Барометрическая формула. Распределение Больцмана.

Идеальный газ в однородном поле тяготения.

Закон Максвелла распределения молекул идеального газа по скоростям и энергиям.

Вопросы

Молекулярная физика

Лекция 15

4. Явления переноса в газах. document.write(' \n'); document.write('on error resume next \n'); document.write('Sub testbar_FSCommand(ByVal command, ByVal args)\n'); document.write(' call testbar_DoFSCommand(command, args)\n'); document.write('end sub\n'); document.write(' \n'); on error resume next Sub testbar_FSCommand(ByVal command, ByVal args) call testbar_DoFSCommand(command, args) end sub c:\Program Files\Physicon\Open Physics 2.5 part 1\content\chapter3\section\paragraph3\test1.htmlc:\Program Files\Physicon\Open Physics 2.5 part 1\content\chapter3\section\paragraph3\task1.htmlc:\Program Files\Physicon\Open Physics 2.5 part 1\content\chapter3\section\paragraph3\tsol1.htmlc:\Program Files\Physicon\Open Physics 2.5 part 1\content\chapter3\lab1.html

В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся закону Максвелла.

Уравнение Клаузиуса 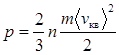, (1)

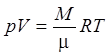
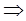
Уравнение Менделеева – Клапейрона 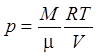(2)

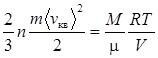
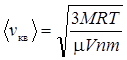
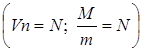
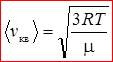, (3)

т.е. средняя квадратичная скорость пропорциональна корню квадратному от абсолютной температуры газа.

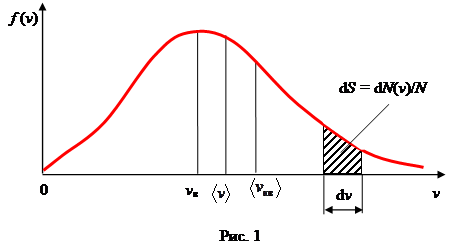
Закон Максвелла описывается функцией f (v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные d v, то на каждый интервал скорости будет приходиться некоторое число молекул d N (v), имеющих скорость, заключенную в этом интервале. Функция f (v) определяет относительное число молекул d N (v) /N, скорости которых лежат в интервале от v до v+ d v, т.е.

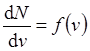- максвелловская функция распределения по скоростям

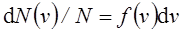, откуда .

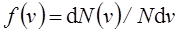Применяя методы теории вероятностей, Максвелл нашел функцию f (v) – закон для распределения молекул идеального газа по скоростям:

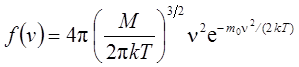. (4)

Относительное число молекул d N (v) /N, скорости которых лежат в интервале от v до v+ d v, находится как площадь полоски d S. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f (v) удовлетворяет условию нормировки

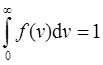. (5)

Наиболее вероятной скоростью v _в называется скорость, вблизи которой на единичный интервал скорости приходится наибольшее число молекул.

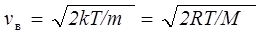. (6)

Средняя скорость молекулы 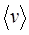(средняя арифметическая скорость):

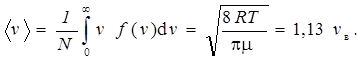(7)

Средняя квадратичная скорость 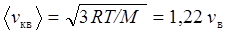(8)

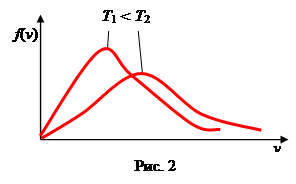
Из формулы (6) следует, что при повышении температуры максимум функ­ции распределения молекул по скоростям сме­щается вправо (значение наиболее веро­ят­ной скорости становится больше). Однако пло­­щадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям растягивается и понижается.

Дата добавления: 2014-01-07