Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду с помощью элементарных преобразований. Метод Гаусса

Деление направленного отрезка в данном отношении.

Теорема 9. Если относительно общей декартовой системы координат на плоскости заданы две различные точки и и точка делит направленный отрезок в отношении, то равна тому из соотношений или, в котором знаменатель не равен нулю, и любому из них, если оба знаменателя. Координаты х, у точки С выражаются через координаты точек А и В соотношениями

Доказательство. Спроектируем точки А, В, С на ось Ох параллельно оси Оу; проекциями будут соответственно точки

Предположим, что точки и различны, т.е., так как при параллельном проектировании сохраняется порядок точек, лежащих на прямой, и отношение отрезков, лежащих на одной прямой, то точка делит направленный отрезок в том же отношении и, значит (§ 5, теорема 1).

Если точки и совпадают, то с ними совпадает и точка, т.е.. формула в этом случае не имеет места, однако формула верна, так как при правая часть обращается в. Аналогично доказывается и остальная часть теоремы.

Следствие. Координаты середины отрезка равны полусуммам его концов.

Теорема 10. Если относительно общей декартовой системы координат в пространстве заданы 2 различные точки и и точка делит направленный отрезок в отношении, то равно тому из отношений

.

В котором знаменатель не равен нулю, и любому из них: если все знаменатели не равны нулю. Координаты точки С через координаты точек А и В выражаются соотношениями

.

Доказательство аналогично предыдущему, здесь только надо проектировать на оси координат параллельно координатным плоскостям.

Следствие. Координаты середины отрезка равны полусуммам координат его концов.

2.1. Элементарные преобразования. Будем называть элементарным преобразованием типа I перестановку двух строк матрицы.

Элементарным преобразованием типа II будем называть следующую операцию: все строки матрицы, кроме одной, остаются прежними, но к этой одной строке прибавляется другая (любая), умноженная на некоторое число.

Утверждение 1. Преобразование, обратное к элементарному, является элементарным, т.е. если матрица В получена из матрицы А с помощью элементарного преобразования, то и матрица А может быть получена из матрицы В с помощью элементарного преобразования.

Доказательство очевидно.

Утверждение 2. Пусть 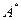- расширенная матрица системы линейных уравнений. Элементарные преобразования этой матрицы не меняют множества решений системы.

Доказательство. Пусть 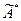- матрица, получившаяся из 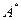с помощью элементарного преобразования и пусть 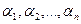- решение исходной системы. Этот же набор чисел будет являться и решением системы с матрицей 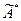- в каждом из двух возможных случаев это очевидно. Значит, решений меньше не стало. А так как обратный переход от 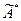к 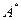осуществляется тоже с помощью элементарного преобразования, то каждое решение системы с матрицей 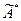будет решением системы с матрицей 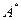. Утверждение доказано.

2.2. Приведение матрицы к ступенчатому виду. С помощью элементарных преобразований можно перейти от исходной матрицы к матрице более простого вида.. Алгоритм следующий.

Пусть дана матрица

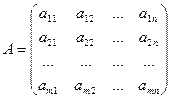
Рассмотрим первый столбец. Пусть в нем есть хотя бы один ненулевой элемент (если такого нет, перейдем ко второму столбцу). Поставим строку, где находится.тот элемент, на первое место (элементарное преобразование первого типа). Теперь прибавим ко 2-й строке 1-ю, умноженную на подходящий коэффициент 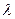, подобрав его так, чтобы элемент 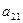стал равен 0: 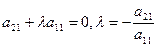. Так же поступим с остальными строками: к 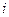-й строке прибавим 1-ю, умноженную на коэффициент 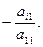Получим матрицу вида

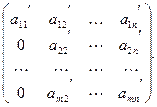
Теперь на время забудем о первой строке. Повторим описанную процедуру для матрицы из элементов 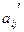, 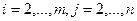. Если во втором столбце, начиная со второй строки, нет ненулевых элементов, перейдем к третьему столбцу. Если же есть ненулевой элемент, поставим его на вторую строку, поменяв строки местами. Затем к остальным строкам, начиная с третьей, прибавим вторую, умноженную на подходящий коэффициент так, чтобы элемент из второго столбца стал равен 0. Матрица примет вид:

.

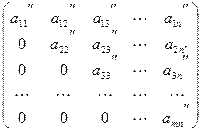Таким способом за конечное число шагов из любой матрицы мы получим матрицу следующего вида:

.

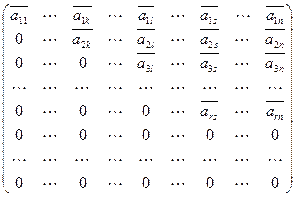Такую матрицу называют ступенчатой (трапецевидной, квазитреугольной). В углу каждой ступеньки стоит ненулевой элемент.

2.3. Метод Гаусса решения систем линейных уравнений (метод последовательного исключения переменных). Пусть дана система линейных уравнений

(*)

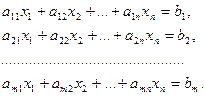Составим расширенную матрицу системы (*):

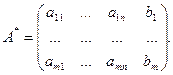
С помощью элементарных преобразований из 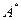мы можем получить другую матрицу, соответствующую другой системе уравнений, но, напомним, множество решений получившейся системы будет совпадать с множеством решений исходной системы (утверждение 2). Значит, если привести матрицу к ступенчатому виду, множество решений не изменится:

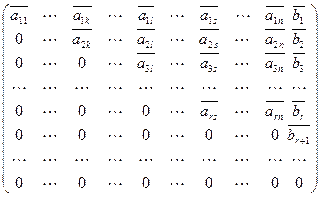
Напомним, что соответствующая система линейных уравнений выглядит так:

....……………………………… (**)

………

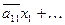
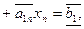
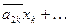
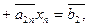
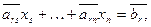
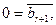
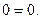
Очевидно, что если в матрице оказалась строка 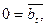причем 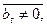то система уравнений несовместна.

Пусть таких строк нет. Тогда неизвестные 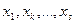назовем главными (они соответствуют нашим «ступенькам»). Количество главных неизвестных равно 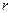. Остальные неизвестные назовем свободными. Очевидно, их .

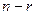Для удобства записи будем считать, что главными оказались переменные , а свободными - 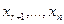(в конце концов, всегда можно переобозначить неизвестные величины). Расширенная матрица системы имеет вид:

,

причем .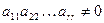

До сих пор мы двигались сверху вниз – это был так называемый прямой ход метода Гаусса. Теперь начнем движение снизу вверх – обратный ход. Прибавим к 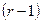-й строке 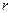-ю, умноженную на подходящий коэффициент 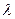, чтобы элемент 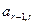стал равен нулю. Этот коэффициент нетрудно найти: 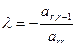. То же самое сделаем с остальными строками. (Заметьте: эти преобразования изменяют только элементы, стоящие в столбцах с номерами от 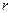до 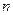). Теперь в 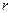-м столбце только элемент 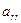не равен нулю.

Поднимемся на строку выше. Так как , то можно добиться того, чтобы все элементы в 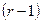-м столбце, кроме самого элемента 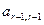, были равны нулю. Постепенно мы дойдем до первой строки и получим матрицу вида

.

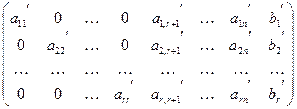Вспомним, что за каждой строкой матрицы стоит линейное уравнение:

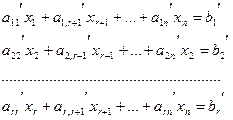
Из этих уравнений сразу получаем выражения для главных неизвестных:

(***)

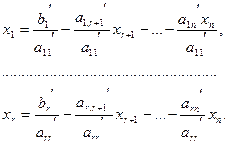Придадим свободным неизвестным произвольные значения. Тогда значения главных неизвестных будут определяться однозначно. Система (***) описывает все решения исходной системы (*).

Сформулируем некоторые, теперь уже очевидные, утверждения.

1. Система (*) совместна 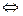в получившейся ступенчатой системе (**) нет уравнений вида 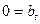, где .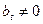

2. Совместная система является определенной 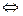в ступенчатой системе (**) .

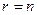3. Однородная система нетривиально совместна (т.е. имеет ненулевое решение) <.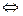

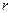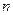Метод Гаусса решения систем линейных уравнений весьма удобен для небольших систем с небольшим количеством неизвестных.. Но в практических задачах, когда коэффициенты при неизвестных даны с определенной точностью и с определенной точностью ищутся решения, при использовании этого метода возникают некоторые проблемы, но это уже вопросы, которые излагаются в курсе «Численные методы».

Пока мы только описали множество решений системы линейных уравнений. О структуре этого множества мы поговорим позднее, когда будет введено понятие линейного пространства и линейной зависимости.

Дата добавления: 2014-01-07