
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ориентированный . Ориентированная плоскость. Площадь
|
|
|
|
Лекция №3
Прошлый раз мы определили ОДСК и ДПСК на плоскости и в пространстве.
Если на плоскости задана ДПСК, то плоскость делится на четыре части I, II, III, VI.
I – это первый квадрант.
II – второй квадрант.
III – третий квадрант.
IV – четвертый квадрант.
 |
Треугольником называется тройка точек. Если эти точки не принадлежат одной прямой, то  - невырожденный. Если принадлежат - вырожденный. Площадь вырожденного
- невырожденный. Если принадлежат - вырожденный. Площадь вырожденного 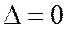 .
.
Ориентированным 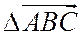 называется упорядоченная тройка точек А, В, С. В обозначении
называется упорядоченная тройка точек А, В, С. В обозначении 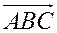 ориентированного
ориентированного  порядок точек определяется порядком их записи: А – первая, В – вторая, С – третья.
порядок точек определяется порядком их записи: А – первая, В – вторая, С – третья.
Плоскость, на которой фиксирован невырожденный ориентированный 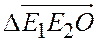 , называется ориентированной.
, называется ориентированной.
Рассмотрим произвольный невырожденный 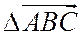 , лежащий на плоскости, ориентированной треугольником
, лежащий на плоскости, ориентированной треугольником  .
.
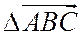 имеет положительную ориентацию, если треугольники
имеет положительную ориентацию, если треугольники  и
и  имеют одинаковую ориентацию, если же
имеют одинаковую ориентацию, если же 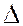 -ки
-ки 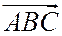 и
и 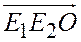 имеют противоположную ориентацию, то
имеют противоположную ориентацию, то 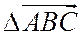 имеет отрицательную ориентацию.
имеет отрицательную ориентацию.
Для наглядности поступают так. Если обходы контуров треугольников 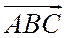 и
и 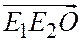 в направлении от первых вершин ко вторым и третьим совершаются в одном направлении (оба против часовой стрелки или оба по часовой стрелке), то треугольники
в направлении от первых вершин ко вторым и третьим совершаются в одном направлении (оба против часовой стрелки или оба по часовой стрелке), то треугольники 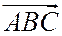 и
и 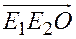 имеют одинаковую ориентацию (рис. 22), а если указанные обходы
имеют одинаковую ориентацию (рис. 22), а если указанные обходы

совершаются в противоположных направлениях (один против часовой стрелки, а другой по часовой стрелке), то треугольники 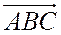 и
и 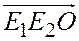 имеют противоположную ориентацию (см.рис.23).
имеют противоположную ориентацию (см.рис.23).
Вырожденному ориентированному треугольнику  не приписывается никакой определенной ориентации (ни положительной, ни отрицательной). Введем на плоскости декартову прямоугольную систему координат; ориентируем ее треугольником
не приписывается никакой определенной ориентации (ни положительной, ни отрицательной). Введем на плоскости декартову прямоугольную систему координат; ориентируем ее треугольником  , где О – начало координат, а
, где О – начало координат, а 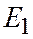 и
и 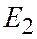 - соответственно единичные точки осей Ох и Оу.
- соответственно единичные точки осей Ох и Оу.
Площадью  невырожденного ориентированного треугольника
невырожденного ориентированного треугольника  , лежащего в плоскости, ориентированной
, лежащего в плоскости, ориентированной 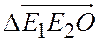 , называется число, абсолютная величина которого равна площади
, называется число, абсолютная величина которого равна площади 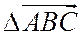 , измеренной масштабным квадратом (т.е. квадратом со стороной
, измеренной масштабным квадратом (т.е. квадратом со стороной 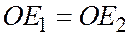 ), и которое положительно, если
), и которое положительно, если 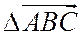 имеет положительную ориентацию, и отрицательную в противном случае.
имеет положительную ориентацию, и отрицательную в противном случае.
Теорема Шаля для площадей. Пусть АВСD – 4 произвольные точки, лежащие на плоскости П. Введем на этой плоскости декартову прямоугольную систему координат хОу. Пусть О – начало координат, а 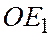 и
и  - масштабные отрезки соответственно осей Ох и Оу
- масштабные отрезки соответственно осей Ох и Оу  . Ориентируем плоскость П ориентированным треугольником
. Ориентируем плоскость П ориентированным треугольником 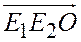 . Тогда
. Тогда
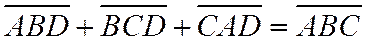 (1)
(1)
Доказательство. Предположим сначала, что 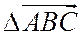 - не вырожденный.
- не вырожденный.
1. Пусть точка D лежит внутри  (см. рис.) тогда:
(см. рис.) тогда: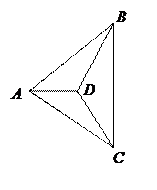
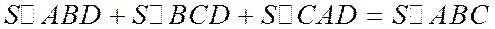 ,
,
или 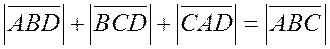 . (2)
. (2)
В рассматриваемом случае все треугольники  ,
, 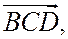
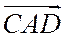 и
и 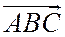 имеют одинаковую ориентацию, поэтому все числа, стоящие под знаком модуля имеют один и тот же знак. Если все они положительны, то знак модуля (по определению модуля или абсолютной величины числа) можно снять. Если все они отрицательны, то при снятии знака модуля перед каждым выражением и слева, и справа надо поставить знак «минус» и после перемены знака опять получим равенство
имеют одинаковую ориентацию, поэтому все числа, стоящие под знаком модуля имеют один и тот же знак. Если все они положительны, то знак модуля (по определению модуля или абсолютной величины числа) можно снять. Если все они отрицательны, то при снятии знака модуля перед каждым выражением и слева, и справа надо поставить знак «минус» и после перемены знака опять получим равенство  .
.
2. Предположим, что точка D лежит в области, ограниченной отрезком АВ и лучами, полученными продолжениями отрезков СА и СВ за точки А и В (см. рис.) Тогда
А и В (см. рис.) Тогда
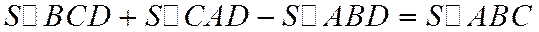 или
или  . (3)
. (3)
В рассматриваемом случае треугольники 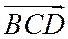 ,
,  и
и 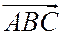 имеют одинаковую ориентацию, а
имеют одинаковую ориентацию, а  , имеет ориентацию, им противоположную. Значит
, имеет ориентацию, им противоположную. Значит 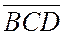 ,
,  ,
,  - числа одного знака, а число
- числа одного знака, а число 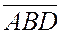 имеет знак, им противоположный. Если, например,
имеет знак, им противоположный. Если, например,
 , то из равенства
, то из равенства 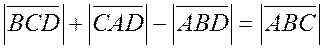 сразу следует
сразу следует 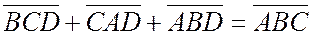 или
или 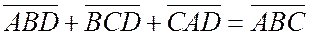 .
.
А если 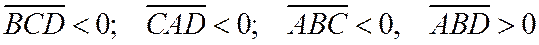 , то после перемены знаков в левой и правой частях
, то после перемены знаков в левой и правой частях  получим
получим 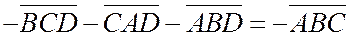 умножаем на -1 левую и правую части, получаем утверждение теоремы
умножаем на -1 левую и правую части, получаем утверждение теоремы 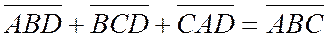 .
.
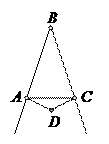 Аналогично доказывается правильность формулы
Аналогично доказывается правильность формулы 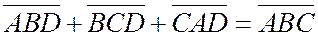 , для случая, когда точка D лежит в области, ограниченной отрезком АС и лучами, полученными продолжением отрезков ВА и
, для случая, когда точка D лежит в области, ограниченной отрезком АС и лучами, полученными продолжением отрезков ВА и
ВС за точки А и С.
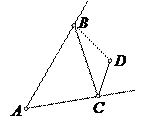 И для случая, когда точка D лежит
И для случая, когда точка D лежит
в области, ограниченной отрезком
ВС и продолжениями отрезков АВ
и АС за точки В и С.
3. Предположим, что точка D лежит внутри угла, вертикального с внутренним углом А треугольника АВС (см. рис.). Тогда:
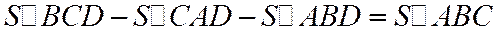
 , или
, или 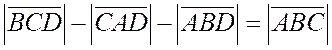 (4)
(4)
Теперь числа 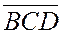 и
и 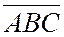 имеют одинаковые знаки, а числа
имеют одинаковые знаки, а числа 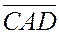 и
и 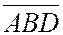 - знаки, им противоположные, поэтому из равенства (4) опять следует равенство (1).
- знаки, им противоположные, поэтому из равенства (4) опять следует равенство (1).
Аналогично доказывается правильность формулы (1) для случая, когда точка D лежит внутри угла, вертикального с внутренним углом В и с внутренним углом С треугольника АВС.
4. Предположим, что точка D лежит на прямой ВС между точками В и С (см. рис.)
 В этом случае
В этом случае  или
или 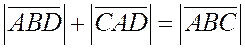 . (5)
. (5)
В рассматриваемом случае треугольники 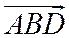 ,
, 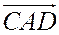 и
и 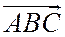 имеют одинаковую ориентацию, поэтому числа
имеют одинаковую ориентацию, поэтому числа  ,
, 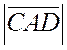 и
и 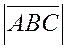 одного знака, и из равенства (5) следует равенство (1), т.к. в рассматриваемом случае
одного знака, и из равенства (5) следует равенство (1), т.к. в рассматриваемом случае 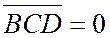 .
.
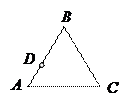
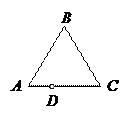 Аналогично доказывается правильность формулы (1) в случае, если точка D лежит на стороне СА между точками С и А или на стороне АВ между точками А и В.
Аналогично доказывается правильность формулы (1) в случае, если точка D лежит на стороне СА между точками С и А или на стороне АВ между точками А и В.
 5. Предположим, что точка D лежит на продолжении отрезка ВС за точку В. Тогда (см. рис. 28)
5. Предположим, что точка D лежит на продолжении отрезка ВС за точку В. Тогда (см. рис. 28) 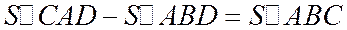 или
или
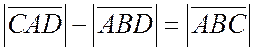 . (6)
. (6)
В рассматриваемом случае треугольники 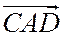 и
и 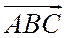 имеют одинаковую ориентацию, а
имеют одинаковую ориентацию, а  имеет ориентацию, им противоположную, поэтому числа
имеет ориентацию, им противоположную, поэтому числа  и
и 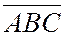 одного знака, а
одного знака, а 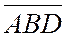 имеет знак, противоположный им. Если, например
имеет знак, противоположный им. Если, например 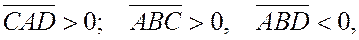 то из равенства (6) сразу следует равенство (1) (т.к.
то из равенства (6) сразу следует равенство (1) (т.к. 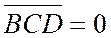 ).
).
 Если
Если  то поменяв в обеих частях равенства (6) знаки опять придем к равенству (1).
то поменяв в обеих частях равенства (6) знаки опять придем к равенству (1).
Аналогично доказывается правильность формулы (1) для случая, когда точка D лежит на продолжении отрезка ВС за точку С, а также когда она лежит на прямой СА (на продолжении отрезка СА за точку А или за точку С).
6. Если точка D совпадает с одной из точек А или В или С, то


7. Остается рассмотреть случай когда точки А, В, С принадлежат одной прямой.

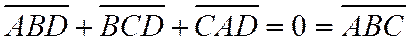
8. Если при этом и точка D принадлежит той же прямой, то соотношение (1) будет 0=0.
 Предположим поэтому, что среди точек А, В, С, D есть три точки не принадлежащие одной прямой. Пусть, например, точки В, С, D не принадлежат одной прямой. Тогда по доказанному, имеем.
Предположим поэтому, что среди точек А, В, С, D есть три точки не принадлежащие одной прямой. Пусть, например, точки В, С, D не принадлежат одной прямой. Тогда по доказанному, имеем.
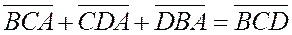 или
или 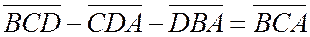 или
или 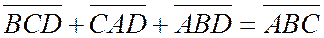 или
или  ЧТД.
ЧТД.
Определение. Выражение 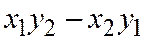 обозначается так:
обозначается так:  и называется определителем второго порядка. Аналогично выражение
и называется определителем второго порядка. Аналогично выражение 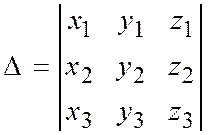 называется определителем третьего порядка. Считается он через определители второго порядка по формуле:
называется определителем третьего порядка. Считается он через определители второго порядка по формуле:
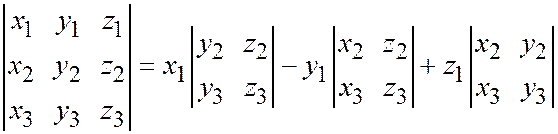 .
.
Теорема 2. Если относительно ДПСК хОу на плоскости заданы точки 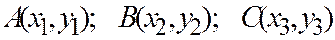 и выбраны единичные масштабные отрезки осей для измерения длин и площадей, то площадь
и выбраны единичные масштабные отрезки осей для измерения длин и площадей, то площадь 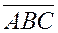 ориентированного треугольника
ориентированного треугольника 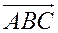 вычисляется через определитель третьего порядка по формуле:
вычисляется через определитель третьего порядка по формуле:
 ,
,
или через определитель второго порядка по формуле:

Доказательство. Сначала предположим, что точка А лежит на оси Ох и не совпадает с началом координат 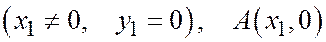 точка В лежит на оси Оу и не совпадает с началом координат
точка В лежит на оси Оу и не совпадает с началом координат 
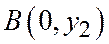 , а точка С совпадает с началом координат
, а точка С совпадает с началом координат 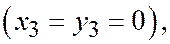
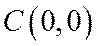 . Тогда
. Тогда

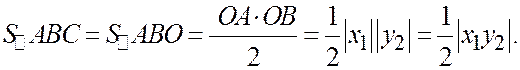
Далее, если 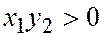 (то есть точки А и В лежат на положительных полуосях Ох и Оу), то треугольники
(то есть точки А и В лежат на положительных полуосях Ох и Оу), то треугольники 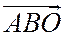 и
и  имеют одинаковую ориентацию, т.е.
имеют одинаковую ориентацию, т.е. 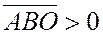 . Если же
. Если же 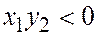 (т.е. точка А лежит левее точки О), то треугольники
(т.е. точка А лежит левее точки О), то треугольники 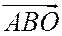 и
и 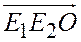 имеют противоположную ориентацию, т.е.
имеют противоположную ориентацию, т.е.  . Таким образом,
. Таким образом,  и
и 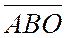 - числа одного знака. Получаем
- числа одного знака. Получаем
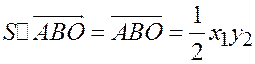 .
.
А через определитель:  . ЧТД.
. ЧТД.
 Пусть А и В – произвольные, а точка С совпадает с началом координат. Обозначим через
Пусть А и В – произвольные, а точка С совпадает с началом координат. Обозначим через 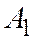 и
и 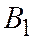 параллельные проекции точек А и В на ось Ох параллельно оси Оу. Применяя теорему Шаля для точек А, В, О,
параллельные проекции точек А и В на ось Ох параллельно оси Оу. Применяя теорему Шаля для точек А, В, О,  будем иметь
будем иметь 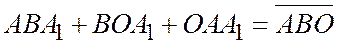 . С другой стороны, ориентация и площадь треугольника не изменится, если одну его вершин переместить по прямой, параллельной стороне, противолежащей этой вершине, следовательно
. С другой стороны, ориентация и площадь треугольника не изменится, если одну его вершин переместить по прямой, параллельной стороне, противолежащей этой вершине, следовательно
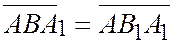
и предыдущее соотношение примет вид:

Применяя теорему Шаля для точек А, 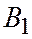 , О,
, О,  , получим
, получим
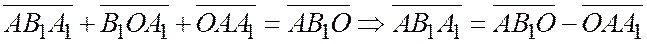
(так как 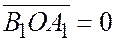 ). Из двух последних соотношений следует, что
). Из двух последних соотношений следует, что
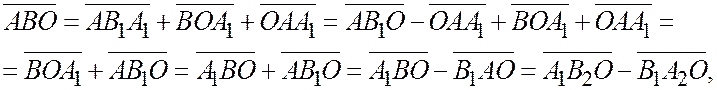 где
где 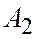 и
и 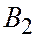 - параллельные проекции точек А и В на ось Оу параллельную оси Ох.
- параллельные проекции точек А и В на ось Оу параллельную оси Ох.
Применяя формулу для вычисления площади треугольника, когда точки А, В лежат на осях координат, имеем:

Площадь через определитель дает
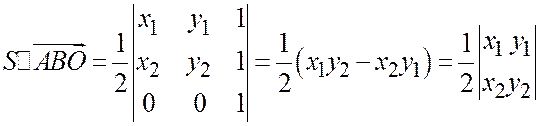 , всё верно.
, всё верно.
Пусть, наконец точки А, В и С занимают на плоскости какое угодно положение. Тогда
 Отнимая из элементов первой и второй строк соответствующие элементы третьей строки и разлагая полученный определитель по элементам последнего столбца, получим:
Отнимая из элементов первой и второй строк соответствующие элементы третьей строки и разлагая полученный определитель по элементам последнего столбца, получим:
 .
.
Следствие 1. Площадь 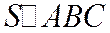 заданного своими вершинами
заданного своими вершинами  ;
; 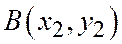 ,
,  относительно ДПСК вычисляются как модуль определителя.
относительно ДПСК вычисляются как модуль определителя.
Следствие 2. Для того, чтобы 3 точки АВС лежали на одной прямой необходимо и достаточно, чтобы 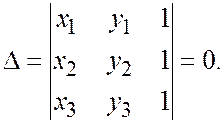
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1875; Нарушение авторских прав?; Мы поможем в написании вашей работы!