И электростатического поля

Энергия заряженного проводника, конденсатора

Для зарядки проводника нужно совершить работу против сил кулоновского отталкивания одноименных зарядов.

Если незаряженному проводнику сообщать заряд малыми порциями d q, переносимыми из бесконечности, где j₀=0. По мере зарядки проводника ёмкостью 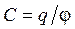его потенциал возрастает

.

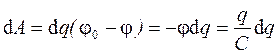
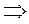
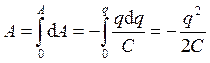Энергия заряженного проводника равна совершенной работе

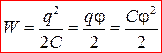. (8)

При зарядке конденсатора малыми порциями 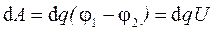по аналогии с зарядкой проводника имеем энергию заряженного конденсатора

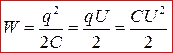. (9)

Используя формулу (9), можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. При изменении расстояния x между пластинами эта сила совершает работу

.

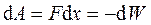
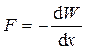
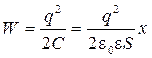
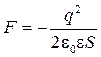Выразим энергию (9) через характеристики электростатического поля

, ,

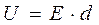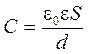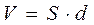- объём между обкладками конденсатора.

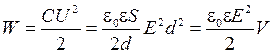
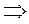
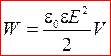. (10)

Объёмная плотность энергии

.

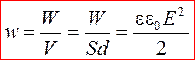Используя связь (2) между напряженностью электрического поля 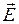и вектором электрического смещения 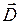полученный результат можно записать так:

. (11)

Объемная плотность энергии конденсатора уже не зависит от каких-либо его геометрических характеристик. Она выражается лишь через характеристики электрического поля конденсатора. Таким образом, энергия конденсатора – это энергия электрического поля, заключенного между его обкладками.

Выражение (11) для плотности электрического поля в какой-либо точке пространства, доказанное нами в случае электрического поля конденсатора, является универсальным. В общем случае энергия неоднородного электрического поля, заключенная в некотором объеме V, рассчитывается через объемный интеграл:

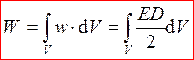, (12)

т.е. носителем энергии является электростатическое поле.

Дата добавления: 2014-01-07