Пучок прямых

Собственным пучком прямых называется множество всех прямых, проходящих через одну точку (центр пучка) и лежащих в одной плоскости.

Несобственным пучком прямых называется множество всех параллельных между собой прямых, лежащих в одной плоскости.

Теорема 2. Для того, чтобы 3 прямые, заданные общими уравнениям

(1)

относительно общей декартовой системы координат, принадлежали одному пучку (собственному или несобственному) необходимо и достаточно, чтобы выполнялось условие.

.

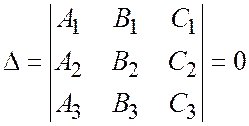Доказательство необходимости. Дано: три прямые (1) принадлежат одному пучку. Требуется доказать, что .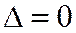

Пусть три прямые, заданные уравнениями (1), принадлежат одному собственному пучку. Это означает, что существует точка , принадлежащая всем этим прямым. Координаты этой точки удовлетворяют всем трем уравнениям (1):

Таким образом столбцы определителя 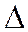линейно зависимы, значит он равен 0.

Если прямые, заданные уравнениями (1), принадлежат одному несобственному пучку, то первые два столбца определителя 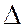пропорциональны, и, значит, он также равен нулю.

Доказательство достаточности. Дано 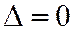. Требуется доказать, что прямые, определяемые уравнениями (1), принадлежат одному пучку.

Предположим, что прямые не принадлежат одному пучку; тогда среди них есть пересекающиеся, ибо если нет пересекающихся, то они параллельны и значит принадлежат несобственному пучку. Пусть, например, пересекаются первая и вторая прямые. Подставляя координаты

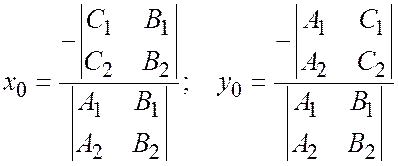
точки пересечения первой и второй прямых в левую часть уравнения третьей прямой, получим

значит, точка пересечения первых двух прямых лежит на третьей прямой, а это значит, что три данные прямые принадлежат одному пучку вопреки предположению.

Теорема 3. Пусть в общей декартовой системе координат заданы две различные прямые 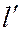и общими уравнениями

Для того, чтобы третья прямая 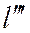заданная также общим уравнением

относительно той же системы координат, принадлежала пучку, определяемому двумя первыми прямыми, необходимо и достаточно, чтобы левая часть уравнения прямой 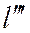была линейной комбинацией левых частей уравнений прямых 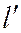и .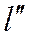

Доказательство необходимости. Дано: прямая 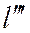принадлежит пучку прямых, определяемых прямым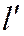и и . Требуется доказать, что найдутся два таких числа 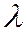и , что будет выполнено тождество, справедливое при всех значениях х и у:

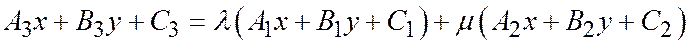
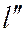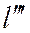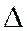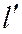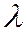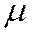В самом деле, если прямые , , принадлежат одному пучку, то (теорема 2); но первые две строки определителя линейно независимы (так как по условию прямые и различны), значит (в силу условия ), третья строка есть линейная комбинация двух первых, т.е. существует такие числа и , что

.

Умножая обе части первого равенства на произвольное число х, обе части второго равенства на произвольное число у, обе части третьего на 1 и складывая, получим

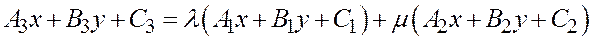. Ч.т.д.

Доказательство достаточности. Дано

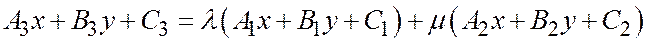(тождество, справедливое при всех значениях х и у). Требуется доказать, что .

В самом деле, из данного тождества следует

а значит, , так как третья строка определителя есть линейная комбинация двух первых. Ч.т.д.

Уравнение

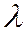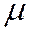где и не равны нулю одновременно, называют уравнением пучка прямых, определяемых двумя различными прямым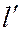и и , общие уравнения которых в общей декартовой системе имею вид

(3)

(Почему уравнение 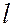является уравнением пучка прямых? (Это доказывается)).

Как было доказано (теорема 3) уравнение всякой прямой пучка, определяемого двумя различными прямым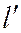и и 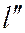, может быть записано в виде : .

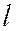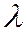Обратно, если уравнение (при и 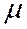, не равных нулю одновременно) есть уравнение первой степени (т.е. коэффициенты при х и у одновременно в нуль не обращаются), то оно является уравнением прямой, принадлежащей пучку прямых, определяемому прямыми 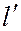и , так как для трех уравнени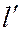й , и 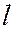условие выполнено. Действительно, составим определитель 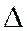из коэффициентов трёх прямых: 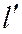, и :

.

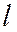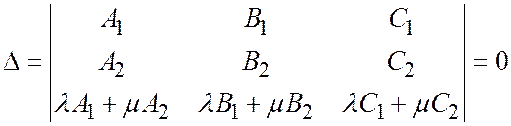Видно, что третья строка определителя есть линейная комбинация первых двух, значит, он равен нулю.

Если прямые и 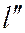пересекаются, то при любых 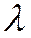и , не равных нулю одновременно, уравнение 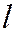будет уравнением первой степени, так как если бы коэффициенты при х и у в этом уравнении оба оказались бы равными нулю, т.е.

то прямые и 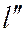были бы коллинеарны, что противоречит предположению о том, что прямые и пересекаются.

Но если прямые и 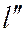параллельны, то коэффициенты при х и у в уравнениях и 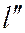пропорциональны, а значит, найдутся числа 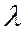и , не равные нулю одновременно, при которых уравнение 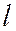не будет уравнением первой степени (например, или при , или при ).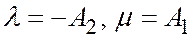

(Но ведь если прямые параллельны – то это несобственный пучок. Ч.т.д.)

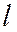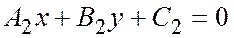Это следует учитывать, если пользоваться уравнением (2) пучка прямых, определяемого двумя параллельными прямыми. В этом случае пучок несобственный. Проверим, будет ли уравнение уравнением первой степени при . Пусть прямые и параллельные, тогда 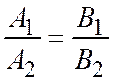, или .

Видно, что уравнение

не является уравнением первой степени, т.к. 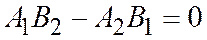. Таким образом с несобственным пучком надо быть осторожными.

Дата добавления: 2014-01-07