Лекция IV-Д-1

Механическая система. Твердое тело. Классификация сил. Центр масс системы. Моменты инерции твердого тела, радиус инерции. Теорема Гюйгенса-Штейнера. (§31-35 Яблонский).

ГЛАВА VI. СИСТЕМА МАТЕРИАЛЬНЫХ ТОЧЕК. ТВЕРДОЕ ТЕЛО. МОМЕНТЫ ИНЕРЦИИ ТВЕРДОГО ТЕЛА § 31. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ТОЧКИ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Системой материальных точек, или механической системой, называют такую совокупность точек, в которой положение или движение каждой точки зависит от положения и движения всех остальных.

Систему материальных точек, движение которых не ограничено никакими связями, а определяется лишь действующими на эти точки силами, называют системой свободных точек. Примером системы свободных точек может служить солнечная система, планеты которой рассматривают в астрономии как материальные точки. Планеты свободно перемещаются по орбитам, зависящим от действующих на них сил.

Система материальных точек, движения которых ограничиваются наложенными на точки связями, называется системой несвободных точек. Примером системы несвободных точек может служить любой механизм или машина, у которых движения отдельных элементов ограничены связями.

Механическая система с неголономными связями называется него лономной системой.

Механическая система с голономными связями называется голо номной системой.

Известно, что механическое действие связей на точки системы выражается силами, называемыми реакциями связей. Таким образом, все силы, Действующие на систему несвободных точек, можно разделить на задаваемые (активные) силы и реакции связей.

Равнодействующую всех задаваемых сил, приложенных к точке M_k несвободной механической системы, условимся обозначать 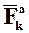a равнодействующую реакций связей - .

Все силы, действующие на точки любой механической системы, как свободной, так и несвободной, можно разделить и по другому признаку: на внешние и внутренние силы.

Внешними называют силы, действующие на точки системы со стороны материальных точек, не входящих в состав данной системы.

Внутренними силами называют силы взаимодействия между материальными точками данной механической системы. Примером внутренних сил могут служить силы упругости, действующие между частицами упругого тела, принятого за механическую систему.

Внешние силы условимся обозначать , а внутренние силы - .

Одна и та же сила может быть как внешней, так и внутренней, в зависимости от того, какая механическая система рассматривается. Так, например, реакции подшипников вала являются внешними силами относительно вала. Эти же реакции относятся к внутренним силам, когда рассматривается вся установка вместе со станиной.

Таким образом, любая сила, действующая на точку механической системы в соответствии с приведенными двумя классификациями сил, является внешней или внутренней и в то же время она является задаваемой силой или реакцией связи.

Движение точек механической системы зависит как от внешних, так и от внутренних сил.

На основании закона равенства действия и противодействия каждой внутренней силе соответствует другая внутренняя сила, равная ей по модулю и противоположная по направлению.

Из этого следует:

1. Главный вектор всех внутренних сил системы и суммы их проекций на координатные оси равны нулю:

, (31.1)

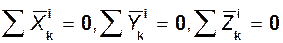. (31.2)

2. Главные моменты всех внутренних сил системы относительно любого центра и координатных осей равны нулю:

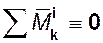, (31-3)

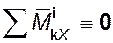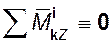,, . (31.4)

Хотя уравнения (31.2) и (31.4) имеют вид уравнений равновесия сил, произвольно расположенных в пространстве, внутренние силы не уравновешиваются, так как они приложены к различным точкам системы и могут вызывать перемещения этих точек относительно друг друга.

Дата добавления: 2014-01-07