
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие производной
|
|
|
|
Пусть функция  определена на промежутке X.
определена на промежутке X.
Возьмем точку 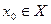 и придадим этому значению некоторое приращение
и придадим этому значению некоторое приращение 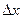 , такое, что новая точка
, такое, что новая точка  . Тогда значение функции изменится от
. Тогда значение функции изменится от 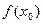 до
до 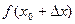 и приращение функции получиться
и приращение функции получиться
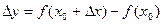
Если существует предел отношения приращения функции  к вызвавшему его приращению независимой переменной
к вызвавшему его приращению независимой переменной 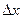 , при стремлении
, при стремлении 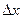 к нулю, т.е.
к нулю, т.е.
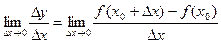
то его называют производной функции  по независимой переменной x в точке
по независимой переменной x в точке . В общем случае, когда производная находится в произвольной точке, аргумент можно не писать. Обозначается производная различными символами:
. В общем случае, когда производная находится в произвольной точке, аргумент можно не писать. Обозначается производная различными символами: 
Итак, производная функции  , при условии существовании предела, определяется по формуле:
, при условии существовании предела, определяется по формуле:
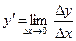
Дифференцирование функции – это операция нахождения производной функции.
Функция называется дифференцируемой в точке  , если она имеет конечную производную в этой точке.
, если она имеет конечную производную в этой точке.
Функция называется дифференцируемой на промежутке  , если она имеет конечную производную во всех точках этого промежутка.
, если она имеет конечную производную во всех точках этого промежутка.
Сравнивая определение и содержание задач, можно сформулировать механический, геометрический и экономический смысл производной.
Механический (физический) смысл производной: скорость V точки в момент времени  есть производная пути S по времени t, т.е.
есть производная пути S по времени t, т.е.
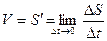
Геометрический смысл производной: угловой коэффициент 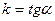 касательной, проведенной к кривой
касательной, проведенной к кривой  в точке
в точке  есть производная
есть производная 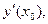 т.е.
т.е.
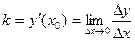 .
.
Используя геометрический смысл производной можно вывести уравнение касательной к некоторой кривой в данной точке. Из курса аналитической геометрии известно уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом: 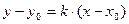 . Заменяя коэффициент k на производную
. Заменяя коэффициент k на производную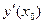 , получим уравнение касательной к кривой
, получим уравнение касательной к кривой  в точке
в точке 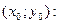
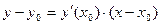
Нормалью к кривойназывается прямая, перпендикулярная касательной в точке касания и уравнение нормали к кривой  в точке
в точке 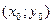 имеет вид:
имеет вид:

Экономический смысл производной: производительность труда p в момент времени  есть производная
есть производная  объема произведенной продукции V по времени t,т.е.
объема произведенной продукции V по времени t,т.е.
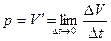
Согласно определению, процесс отыскания производной функции  в точке
в точке предполагает выполнение следующих действий:
предполагает выполнение следующих действий:
1. Значению  дать произвольное приращение
дать произвольное приращение  , тогда новое значение аргумента окажется равным
, тогда новое значение аргумента окажется равным 
2. Вычислив значения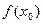 и
и 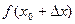 , отыскать приращение функции
, отыскать приращение функции 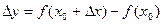 .
.
3. Найти отношение 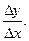
4. Найти 
Пример. Найти производную функции  в точке
в точке 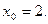
Решение. 1) дадим значению  приращение
приращение  , тогда новое значение аргумента окажется равным
, тогда новое значение аргумента окажется равным 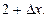
2) учитывая, что 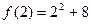 , а
, а 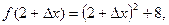 вычислим приращение функции
вычислим приращение функции 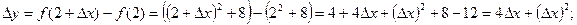
3) Составляя отношение получаем
получаем 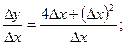
4) Найдем предел Имеем:
Имеем: 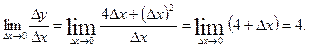
Итак, 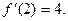
Рассмотрим, как связаны два важнейших свойства функции – непрерывность и дифференцируемость.
Теорема 5.1. Если функция  дифференцируема в некоторой точке
дифференцируема в некоторой точке  , то она и непрерывна в этой точке.
, то она и непрерывна в этой точке.
Доказательство. По условию теоремы, функция  дифференцируема в точке
дифференцируема в точке  , т.е. она имеет конечную производную, а именно существует предел:
, т.е. она имеет конечную производную, а именно существует предел:
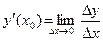 , где
, где 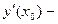 конечна и не зависит от
конечна и не зависит от 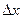 .
.
Используя третью запись предела, имеем:
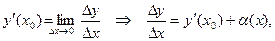 где
где  бесконечно малая функция.
бесконечно малая функция.
Выразим 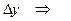
 (т.к.
(т.к. 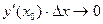 и
и 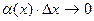 при
при  ).
).
Таким образом, 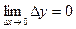 . По определению непрерывности функция
. По определению непрерывности функция  непрерывна в точке
непрерывна в точке . Теорема доказана
. Теорема доказана
Обратное утверждение в общем случае неверно, т.е. если функция непрерывна в какой-то точке, то она не обязательно будет дифференцированной в этой точке. В качестве доказательства приведем пример функции  ,которая непрерывна в точке
,которая непрерывна в точке 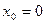 , но не дифференцируема в этой точке.
, но не дифференцируема в этой точке.
Используя определение производной, приведем примеры дифференцирования некоторых основных элементарных функций.
Пример…  const. Область определения этой функции множество всех действительных чисел
const. Область определения этой функции множество всех действительных чисел  . Зафиксируем произвольную точку
. Зафиксируем произвольную точку  . Дадим аргументу x в точке
. Дадим аргументу x в точке произвольное приращение
произвольное приращение  , получим точку
, получим точку Найдем значения функции в точках
Найдем значения функции в точках  и
и  получим
получим 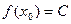 ,
,  . Поэтому,
. Поэтому, 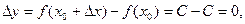 а следовательно,
а следовательно,  и
и 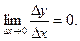 Таким образом,
Таким образом, 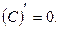
Пример … Область определения этой функции множество всех действительных чисел
Область определения этой функции множество всех действительных чисел  . Зафиксируем произвольную точку
. Зафиксируем произвольную точку  . Дадим аргументу x в точке
. Дадим аргументу x в точке произвольное приращение
произвольное приращение  , получим точку
, получим точку Найдем значения функции в точках
Найдем значения функции в точках  и
и  получим
получим  ,
,
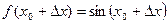 .
.
Поэтому, 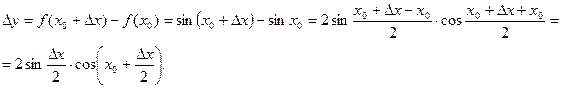
Следовательно, 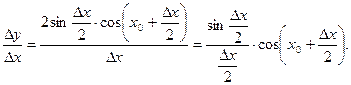
Воспользовавшись первым замечательным пределом и непрерывностью функции 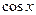 , окончательно получаем:
, окончательно получаем:

Таким образом, 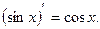
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 538; Нарушение авторских прав?; Мы поможем в написании вашей работы!