Выпуклость и вогнутость графика функции. Точки перегиба

Лекция 6.4. Общее исследование функций с помощью производной

План:

1. Выпуклость и вогнутость графика функции. Точки перегиба.

2. Асимптоты графика функции.

3. Общая схема исследования функции.

Кроме точек экстремума достаточно важными для построения графика функции являются точки перегиба. В этих точках происходит изменение формы графика функции.

Функции называется выпуклым вниз на интервале , если для любых двух точек выполнено неравенство

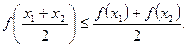
Функции называется выпуклым вверх на интервале , если для любых двух точек выполнено неравенство

Определение для графиков может быть дано в более наглядной форме.

График функции называется выпуклым вверх на интервале , если он расположен ниже любой своей касательной на этом интервале.

График функции называется выпуклым вниз на интервале , если он расположен выше любой своей касательной на этом интервале.

Замечание. Вместо термина «выпуклость вниз (вверх) иногда употребляют термин «вогнутость (выпуклость)».

Точкой перегиба называется точка графика функции, где меняется направление выпуклости. На рис. 31а) изображен график функции 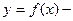выпуклый вверх, на рис. 31б)-график функции выпуклый вниз, на рис. 31в) изображен график функции с точкой перегиба

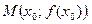
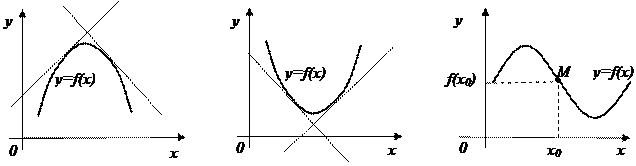а б в

Рис.31

Интервалы выпуклости вверх и вниз находят с помощью следующей теоремы.

Теорема… (достаточное условие выпуклости). Если во всех точках интервала функцияимеет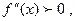то график функции на этом интервале выпуклый вниз; если то график функции на этом интервале выпуклый вверх.

Итак, 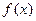– выпукла вниз 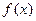– выпукла вверх

Обратное утверждение верно, но при некотором ослаблении условия.

Теорема… (необходимое условие выпуклости). Если во всех точках интервала дважды дифференцируемая функция выпукла вниз, то для всех точек из этого интервала если функция выпукла вверх, то для всех точек из этого интервала

Итак, 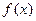– выпукла вниз 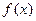– выпукла вверх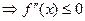

Для нахождения точек перегиба графика функции используется следующая теорема.

Теорема… (достаточное условие существования точек перегиба).

Если вторая производная 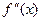при переходе через точку , в которой она равна нулю или не существует, меняет знак, то точка графика 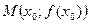есть точка перегиба.

Доказательство основано на условии выпуклости и вогнутости. При смене знака 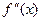с «+» на «–» график функции меняет выпуклость вниз на выпуклость вверх, значит, 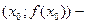точка перегиба. Аналогично рассматриваются и другие случаи.

Замечание … Если критическая точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба.

Замечание.. График функции может менять направление выпуклости не только при переходе через точку перегиба, но и при переходе через точку разрыва. Например, у графика функции точка является точкой разрыва второго рода. Но слева от точки , т.е при вторая производная 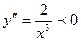и график выпуклый вверх, а справа от , т.е при вторая производная 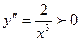и график выпуклый вниз.

Дата добавления: 2014-01-07