Направление потока за турбинной решёткой

Направление потока определяется выходными кромками лопаток рассматриваемого ЛВ, но угол выхода потока из ЛВ, как правило, не равен лопаточному углу. Выясним причины этого расхождения. Проведём выкладки для СА, но для РК они будут аналогичны, т.к. и у СА, и у РК каналы криволинейны, сужаются, есть косой срез.

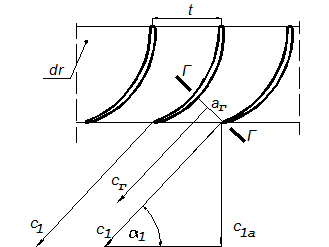Скорость в горле межлопаточного канала с_Г, она перпендикулярна сечению Г – Г.

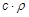Запишем уравнение неразрывности для потока между сечениями Г – Г и 1 – 1. Примем во внимание, что осевая составляющая абсолютной скорости , а произведение - плотность тока.

G₁ = G_Г; .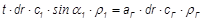

Отсюда .

Отметим, что , где 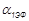- эффективный угол на выходе из СА. Угол имеет тот смысл, что если бы выходные кромки лопаток СА были бесконечно тонкими, то .

Окончательно . Угол очень важен, т.к. он определяет работу, производимую газом в РК.

Проанализируем полученную зависимость.

Во-первых, a₁ зависит от от a_1ЭФ прямопропорционально, т.е. чем выше , тем больше .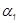

Во-вторых, a₁ зависит от отношения плотностей тока в указанных сечениях. Рассмотрим три возможных случая.

1 случай. Перепад давлений на СА докритический. В этом случае весь поток дозвуковой, в любой точке потока абсолютная скорость меньше критической (). Следовательно, при течении газа от сечения 0-0 до сечения Г- Г скорость потока растёт и в горле канала будет наибольшей. Дальше скорость потока уменьшается, т.к. площадь поперечного сечения струи возрастает. При значениях приведённой скорости скорость потока изменяется интенсивнее, чем его плотность, следовательно, изменение плотности тока будет определяться изменением скорости. Поскольку в сечении Г- Г скорость самая высокая, то , следовательно, . Введём - специальный параметр, который характеризует добавку к 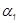по сравнению с ; угол отклонения потока в косом срезе межлопаточного канала СА. Тогда можно сказать, что .

2 случай. Пусть перепад давления на СА будет приблизительно критическим. В этом случае в области сечения Г- Г 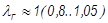. Для таких режимов течения интенсивность изменения плотности и скорости приблизительно одинаковы. Поэтому , следовательно, .

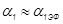3 случай. Перепад давления на СА сверхкритический. В этом случае скорость от сечения 0-0 до Г- Г и в горле межлопаточного канала . Т.к. далее перепад давлений остаётся очень большим, площадь поперечного сечения струи увеличивается, скорость потока возрастает и становится сверхзвуковой. В области сверхзвуковых течений плотность потока меняется интенсивнее, чем скорость, поэтому изменение плотности тока определяется изменением плотности газа , следовательно, , .

Отношение , где 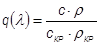- приведённый расход, - плотность тока в потоке, - максимально возможная плотность тока.

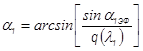
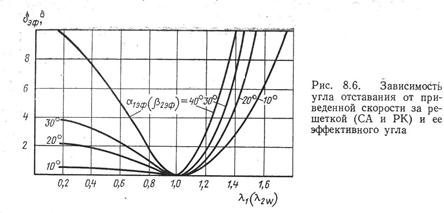
Выводы:

- в СА, состоящем из сужающихся межлопаточных каналов, при больших перепадах давлений можно получить сверхзвуковую скорость потока;

- угол отклонения потока в косом срезе межлопаточного канала тем больше, чем больше отличается перепад давлений на СА от критического в ту или иную сторону.

Дата добавления: 2014-01-07