П.1.1. Высказывания

Лекция 1. Логика высказываний

Высказывание – повествовательное предложение, относительно которого известно, что оно либо истинно, либо ложно.

Примеры:

1) «Марс дальше от Солнца, чем Венера» является истинным высказыванием.

2) «» - ложное высказывание.

Не всякое предложение является высказыванием:

а. Вопросительное предложение – «Какого цвета же книга?»;

б. Восклицательное предложение – «Стоп!»;

в. Повествовательное предложение – «Он сероглаз»; «»;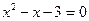

г. Определения – «Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны»

Предложения а – г не являются высказываниями, так как не содержат никакого значения истинности. Высказывания делятся на простые и сложные. Высказывание будем считать простым (элементарным), если никакая его часть не является высказыванием.

Высказывания будем обозначать строгими латинскими буквами . Для обозначения истинности используются символы «и» и «1», а для обозначения ложности – символы «л» и «0». Из простых высказываний с помощью небольшого числа операций строятся сложные высказывания.

П.1.2. Логические операции. Таблица истинности.

Логическая операция может быть описана таблицей истинности, указывающей, какие значения примет сложное выражение при всех возможных значениях простых выражений.

Логические операции имеют специальные названия и обозначаются следующим образом:

Название	Прочтение	Обозначение
Отрицание, инверсия	не, наверно, что	, ┐,
Конъюнкция, логическое умножение	и, а, но, хотя	&, ,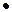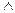
Дизъюнкция, нестрогая дизъюнкция, логическое сложение	или
Разделительная (строгая) дизъюнкция	либо	,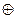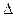
Импликация, следование	если…, то	,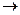
Эквивалентность, эквиваленция, равнозначность	тогда и только тогда, когда	~, ,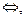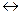

Введем перечисленные логические операции формальным образом.

1. Операция отрицания.

Отрицанием высказывания называется новое высказывание, которое истинно, когда 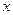- ложно, и ложно, когда 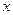- истинно.

Логическая операция отрицание задается следующей таблицей истинности:

Пример 1. : «Число 326 – четное».

Отрицание : «Неверно, что число 326 – четное».

Пример 2. : «Число 417 делится на 4».

: «Число 417 не делится на 4».

Пример 3. 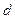: «Все студенты имеют дома компьютеры.»

: «Некоторые студенты не имеют дома компьютеры».

2. Операция конъюнкции.

Конъюнкцией высказывани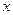й и 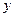называется новое высказывание 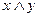, которое истинно только тогда, когда оба высказывания 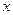и 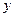истинны, и ложно, когда хотя бы одно из 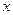и 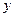ложно.

Таблица истинности конъюнкции:

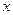
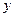
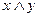
Пример 4. 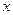: «6 делится на 2».

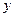: «6 делится на 3».

Конъюнкция 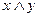: «6 делится на 2 и 3».

Пример 5. : «Студент Петров любит математику».

: «Студент Петров не любит физику».

Конъюнкция : «Студент Петров любит математику, но не любит физику».

3. Операция дизъюнкции.

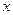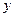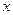Дизъюнкцией (логическим сложением) двух высказываний и называется новое высказывание , которое считается истинным, если хотя бы одно из высказываний и 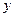истинно, и ложным, если оба они ложные.

Таблица истинности дизъюнкции:

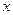
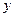
Пример 6. 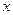: «число три делит число шесть».

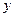: «число шесть больше, чем число три».

Дизъюнкция : «Число три делит число шесть или число шесть больше, чем число три».

Союз «или» может применяться в речи и в другом «исключающем» смысле. Тогда он соответствует другому высказыванию – разделительной, или строгой дизъюнкции.

Исключающему «или» соответствует следующая таблица истинности:

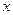
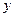
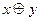
Для разделительной дизъюнкции часто используют связку «либо».

Пример 7. : «Кошка охотится за мышами».

: «Кошка спит на диване».

: «Кошка охотится за мышами, либо спит на диване».

4. Операция импликации.

Импликацией двух высказывани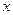й и 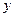называется новое высказывание 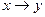, которое считается ложным, когда 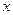истинно, а 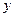ложно, и истинным во всех остальных случаях.

Таблица истинности импликации:

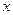
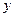
Высказывание 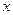называется условием, посылкой или антецедентом, высказывание 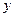- следствием, заключением или консеквентом.

Пример 8. 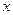: «число 136 делится на 3».

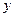: «число 136 – составное».

Импликация 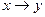: «Если число 136 делится на 3, то оно составное».

Пример 9. : «».

: «крокодилы летают».

Импликация 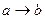: «Если , то крокодилы летают».

Это высказывание в соответствии с отрицанием является истинным несмотря на то, что в нем посылка и следствие не связаны по содержанию.

5. Операция эквиваленции.

Эквиваленцией двух высказывани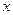й и 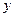называется новое высказывание 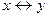, которое истинно, когда ба высказывания 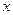и 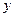либо одновременно истинны, либо одновременно ложны, и ложно во всех остальных случаях.

Пример 10. 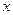: «Число 3153 делится на 3».

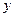: «Сумма цифр числа 3153 делится на 3».

Эквиваленция 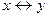: «Число 3153 делится на 3 тогда и только тогда, когда сумма цифр его делится на 3».

Логическая наука, занимающаяся высказываниями, называется алгеброй высказываний. Название это становится понятным, если «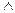» называть произведением, а «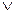» - сложением. Мы как бы перемножаем и складываем высказывания. Алгебра высказываний строится так же, как и многие другие разделы математики: арифметика, алгебра, геометрия и т.д.

Дата добавления: 2014-01-07