П. 5.4 Формулировка обратных и противоположных теорем

Рассмотрим четыре схемы теорем:

1.

2.

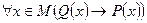
3.

4.

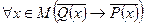
Две теоремы, у которых условие одной является заключением другой, а условие второй заключением первой, называется взаимно обратимыми, т.е. (1) и (2) взаимно обратимы и (3) и (4) – также взаимно обратимы. Первая теорема обычно называется прямой теоремой, а вторая – обратной. Две теоремы, у которых условие и заключение одной являются отрицанием условия и заключение другой, называются взаимно противоположными. Теорема (1) и (3), (2) и (4) – взаимно противоположными. Прямая и обратная теоремы в общем случае не равносильны, то есть одна из них может быть истинной, а другая ложность. Но теоремы (1) и (4), (2) и (3) всегда равносильны. Это можно доказать.

.

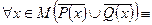
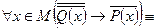
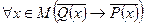5.5 Формулировка необходимых и достаточных условий.

В теореме , предикат Q(x) логически следует из предиката Р(х), поэтому Р(х), называют достаточным условием для Q(x), а

Q(x) – называют необходимым условием для Р(х):.

Если теорема имеет вид 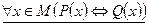, то можно записать

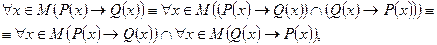
то есть Р(х) – является необходимым и достаточным условием для Q(x), а Q(x) необходимо и достаточно для Р(х).

Пример:

1) Рассмотрим утверждение: «Если число натуральное делится на 4, то оно четное». Оно делимое.

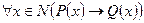
: «делимость х на 4»

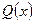: «число х четное»;

Следовательно, делимость числа на 4 является достаточным условием его четности, а четность числа – необходимым условием его делимости на 4.

2) «В следующих предложениях поставить слова «необходимо, но недостаточно», «достаточно, но необходимо», «не необходимо и недостаточно» или «необходимо и достаточно».

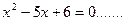«Для того чтобы , чтобы ».

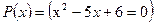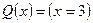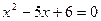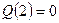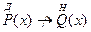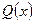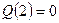Пусть , . Корни уравнения равны . Рассмотрим . При , , ,то есть . Следовательно, для не является необходимым. Теперь рассмотрим противоположную импликацию . Здесь при : ; ; и при 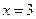: , , 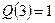, 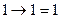вторая импликация верна. Значит для 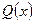является достаточным условием. Итак предложение может быть сформулировано «Для того, чтобы 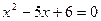достаточно, но не обходимо, чтобы ».

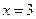Вопросы и задания:

1. Введя подходящие одноместные предикаты на соответствующих областях, переведите следующие высказывания на язык логики предикатов:

а) Все рациональные числа действительные;

б) Некоторые рациональные числа действительны;

в) Некоторые рациональные числа не являются действительными.

2. Записать на язык логики предикатов, следующие определения:

а) Строго монотонной последовательности:

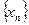«называется вырастающей (убывающей), если при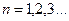 . Вырастающие и убывающие последовательности называются строго монотонными».

б) Периодической функции:

«Функция называются периодической, если существует такое число Т 0, что при любом х из области определения функции числа и 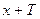принадлежат этой области и выполняется условие »

в) Монотонно вырастающей функции:

«Функция называется монотонно вырастающей, если из неравенства следуют, что ».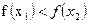

3. Пусть означает «х – простое число», означает «х – четное число», 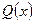: «х – нечетное число», 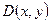: «х делит у». Переведите на русский язык следующие символические записи на языке логики предикатов, учитывая, что переменные х и у пробегают множество натуральных чисел:

а) ;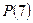

б) ;

в) ;

г);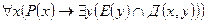

д) .

4. Доказать несправедливость утверждений:

а) «Если функция дифференцируемая в точке 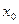, то она имеет в этой точке локальный экстремум».

б) «Если дифференцируемая функция имеет в точке 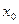вторую производную, равную нулю , то точка 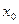- точка экстремума функции».

5. Используя приведенную основную теорему, сформулировать к ней обратную, противоположную и обратную к противоположной теореме.

а) «Если в четырехугольнике диагонали взаимно перпендикулярны, то этот четырехугольник ромб».

б) «Если числовой ряд сходится, то его n -ый член стремится к нулю при ».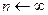

в) «Во всяком параллелограмме есть центр симметрии».

6. Дополнить следующие предложения словами «необходимо и достаточно», «необходимо и недостаточно», «достаточно, но необходимо», или «не необходимо и недостаточно».

а) «Для того чтобы два треугольника были равны,...., чтобы все углы одного треугольника были равны соответствующим углам другого».

б) «Для того чтобы все стороны многоугольника были равны,.., чтобы этот многоугольник был правильным».

в) «Для того чтобы четырехугольник был прямоугольником,..., чтобы все его углы были равны».

Дата добавления: 2014-01-07