
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В. “Павутиноподібна” модель
|
|
|
|
Ця модель описує процеси встановлення цінової рівноваги на конкурентному ринку за умов, коли споживач визначає свій попит на основі діючої ціни, а виробник встановлює пропозицію на основі ціни у попередній момент часу.
Модель динамічна, з часом, що змінюється дискретно. Позначимо такий час t, t = 1, 2,… T.
Нехай  - попит на товар у момент часу t,
- попит на товар у момент часу t, 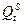 - пропозиція цього товару, Pt – ціна у момент часу t. Тоді, згідно із зробленими припущеннями,
- пропозиція цього товару, Pt – ціна у момент часу t. Тоді, згідно із зробленими припущеннями,  = F (Pt),
= F (Pt), 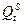 = G (Pt- 1 ). Припустимо, що ринок знаходиться у стані рівноваги у кожен з моментів часу t:
= G (Pt- 1 ). Припустимо, що ринок знаходиться у стані рівноваги у кожен з моментів часу t:
F (Pt) = G(Pt- 1 ),
розв’язавши це рівняння відносно Pt, одержимо
Pt = g (Pt- 1 ), t = 1, 2, … (6.5)
Будемо вважати, що  , якщо
, якщо 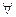 P (1) та P (2)
P (1) та P (2)
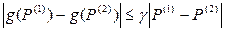 .
.
За відомою теоремою Банаха для збіжності { Pt } достатньо, щоб γ < 1. Отже, якщо 0 < γ < 1, послідовність { Pt } збігається до сталої ціни  , у іншому випадку можливе необмежене збільшення ціни або її коливання.
, у іншому випадку можливе необмежене збільшення ціни або її коливання.
Зокрема, у частковому випадку, коли
F (Pt) = a - bPt, G (Pt- 1 )= c + dPt- 1,
маємо:
Pt =α + β Pt- 1, t = 1, 2,… T,
де
 ;
; 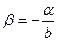 .
.
Цінова стабілізація спостерігатиметься, якщо  .
.
Дійсно, тоді
 , t = 1, 2,…
, t = 1, 2,…
та
 , t → ∞.
, t → ∞.
Якщо 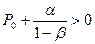 , то Pt – спадає (рис. 6.1).
, то Pt – спадає (рис. 6.1).
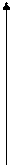 Pt
Pt
 | ||||
 | ||||
 |
t
Рис. 6.1. Випадок спадних цін
Якщо  , то Pt – зростає (рис. 6.2).
, то Pt – зростає (рис. 6.2).
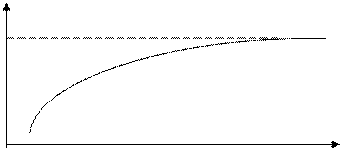 |
Рис. 6.2. Випадок зростаючих цін.
В. Модель Самуэльсона.
Це – приклад моделі нерівноваженого конкурентного ціноутворення. Модель – динамічна, з неперервною зміною часу. Нехай P(t) – ціна на певний товар у момент часу t, 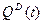 - попит на цей товар у момент часу t (залежить від Р),
- попит на цей товар у момент часу t (залежить від Р), 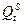 (t) – пропозиція у цей момент часу (також може залежати від Р, можливий лаг). Тоді
(t) – пропозиція у цей момент часу (також може залежати від Р, можливий лаг). Тоді
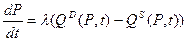
нелінійне диференціальне рівняння (рівняння Самуельсона).
Застосування:
а) теоретико-аналітичне (особливо – аналіз інфляції);
б) прикладне (прогноз цін).
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1917; Нарушение авторских прав?; Мы поможем в написании вашей работы!