Одержана модель

З (9.2) випливає рівність

Звідси

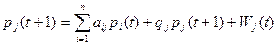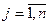, , (9.2)

t = 0, 1, 2,…

де .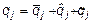

, ,

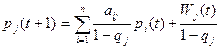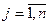t = 1, 2,…

, ,

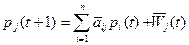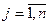t = 1, 2,…

,

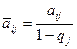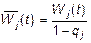
є узагальненням відомої павутиноподібної моделі. Для стабілізації цін у ній достатньо, щоб виконувались умови стискаючих відображень: .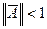

Останнє означає, що для матриці 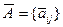має виконуватись хоча б одна з умов:

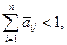
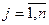, (9.3)

або ж

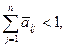
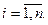(9.4)

За невиконання обох цих умов можливе стале зростання цін –структурна інфляційна криза. Невиконання умови (9.3) означає наявність галузей з великими виробничими витратами, а невиконання (9.4) – галузей з великим виробничим попитом на продукцію, яку вони виробляють. Особливо небезпечно, коли ані (9.3), ані (9.4) не виконуються для одних і тих самих галузей. Тоді ціни на їх продукцію можуть зростати за законом геометричної прогресії. (Cеред таких галузей в Україні на початку 90-х років була – вугільна промисловість).

Розглянута модель дозволяє також пояснити зростання неплатежів як наслідок протиріччя між ціною та собівартістю продукції.

Нехай

неплатежі

власні витрати

.

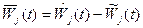Тоді

,

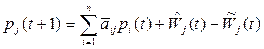або ж

.

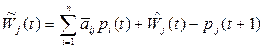Якщо ціна p_j (t+ 1 ) зростає повільніше від оцінки вартості продукції галузі , тоді 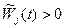. Причини: занадто низький попит на продукцію за її великої ціни (згадаймо ефект заміщення), вихід виробника на світові ринки (він не зможе конкурувати, запропонувавши там товар обмеженої якості за ціною, яка перевищує світову). Величина таких неплатежів може бути значною. Наприклад, у 1996 р. в Україні вони становили близько 25% сукупного суспільного продукту або ж 80% зафіксованих на той час неплатежів.

Іншим чинником, що суттєво впливає на динаміку цін (особливо за умов сильної інфляції), є інфляційні очікування. Їх дію можна, частково, продемонструвати за допомогою раніш розглянутої динамічної міжгалузевої моделі (9.2), поклавши замість цін p_i(t) (у її правій частині) очікувані значення цих цін (а саме вони здебільшого використовуються при довгостроковому прогнозуванні цін суб’єктами господарювання). Якщо ці очікувані значення 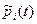будуть більшими за 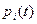, величина 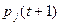також буде зростати швидше (бо права частина - більша). Отже, інфляційні очікування можуть стати суттєвим, а, іноді, і головним чинником, який визначає динаміку цін. Для опису впливу очікувань на ціни існують і спеціалізовані математичні моделі. Одна з них – модель Кейгана (Cagan):

,

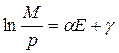де М – номінальна грошова маса, р – рівень цін (дефлятор), Е – інфляційні очікування, α, γ – параметри моделі.

Як правило, α < 0, γ > 0: сильні інфляційні очікування “стискають”, тобто зменшують реальну грошову масу 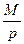. Існують різні способи оцінювання очікувань, особливо в динаміці. Найпростіший з них, коли очікування – це середні темпи зростання цін за певний проміжок часу [t; t - τ], що безпосередньо передує даному часовому моменту t:

,

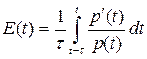де p(t) – функція зміни ціни у часі, p′ - її похідна.

Підставивши цю рівність у попередню, одержимо рівняння:

.

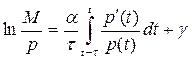Якщо позначити ln M = m(t), ln p(t)= y (t) та звернути увагу на те, що 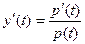, маємо:

, ,

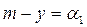
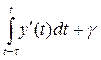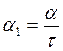або ж

,

.

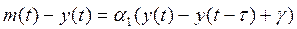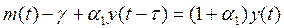Звідси

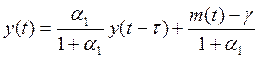. (9.5)

Зазначимо, що α₁ < 0, повинно виконуватись α₁ ≠ -1 (інакше рівняння не визначатиме динаміку певного процесу зміни цін).

З (9.5) одержимо остаточне співвідношення:

.

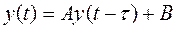
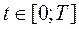Ця модель називається хвильовою моделлю.

Її особливості:

1) якщо А > 0 (α₁ < -1), то зростання цін у момент t – τ призведе до зростання цін у момент часу t. Збільшення грошової маси призводить до уповільнення зростання цін.

2) Якщо А < 0 (α₁ > -1), то зростання цін у момент t – τ призведе до зменшення цін у момент часу t і навпаки. Збільшення грошової маси прискорює зростання цін.

Характерні коливання цін, що виникають згідно цієї моделі дістали назву “інфляційні хвилі”.

Це, звичайно, досить рідкісне макроекономічне явище.

Інший випадок, коли 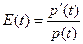. Тоді з моделі Кейгана одержимо рівняння

m – y = α y′ + γ.

За умови y (0) = y⁰ його розв’язком буде

.

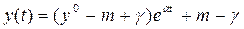Враховуючи, що α < 0, за достатньо великих t e^αt ≈ 0 та y ≈ m – γ.

Узагальненням цього співвідношення стала лінійна модель:

Y = am + be + c,

де а, b, c – сталі коефіцієнти, e = ln E (t). За допомогою лінійної моделі вдалось, зокрема, достатньо точно відобразити інфляційні процеси в Україні у 1993 році.

Тема 10. Комплексні макроекономічні моделі

1. Модель Хікса-Хансена.

2. Класична модель.

3. Кейнсіанська модель та її модифікації.

4. Динамічна макромодель перехідної економіки.

Раніш розглянуті макромоделі відображають окремі економічні процеси - зміни реальних значень макроекономічних показників, зміну цін, тощо. При дослідженні макроекономічних процесів виникає потреба одночасного, узгодженого розгляду різних сегментів національного ринку та різнопланових явищ, які на них відбуваються. Для цього розроблені комплексні макроекономічні моделі. Розглянемо деякі з них.

У моделі Хікса-Хансена розглянуто реальний сектор та ринок робочої сили. Для опису реального сектора застосовано модель IS-LM:

Y = min (kI(i)), max (0, ),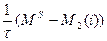

де Y – величина реального ВВП, I(i) – функція інвестиційного попиту, і – норма процента (середня кредитна ставка), M₂(i) – спекулятивний попит на гроші, M^S - пропозиція грошей. Коефіцієнт τ визначає швидкість обертання грошей та наявність власних вільних коштів у суб’єктів господарювання, k – фондоємність виробництва.

Фактично, це – залежність обсягу створеного ВВП Y від існуючих фінансових обмежень.

Як правило, використовуються наступні залежності:

,

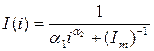де I_m - найбільший обсяг інвестицій, якого можна досягнути за нульових значень кредитної ставки (технологічна потреба у інвестиціях).

Тут функція інвестиційного попиту вважається подібною до функції попиту на товари першої необхідності з обмеженим граничним споживанням, α₁ та α₂ –її коефіцієнти;

,

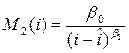де 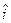- рівень “ліквідної пастки” – відсоток гарантованих доходів по високонадійним спекулятивним операціям (наприклад, операціям з державними цінними паперами).

Взаємозв’язок між реальним сектором та ринком робочої сили визначається за допомогою виробничої функції

Y = F(L).

Це може бути відома функція типу Коба-Дугласа:

Y = a₀ L^γ , 0 < γ < 1,

де а₀ – коефіцієнт (залежить від наявного капіталу), або ж інша залежність.

Ринок робочої сили визначається кривими попиту на працю та пропозиції праці:

L^D = G ₁ (W),

L^S = G₂ (W),

де W – реальна оплата праці (ціна робочої сили). Найчастіше вважається, що

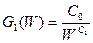, C₀, C ₁ > 0,

0, якщо W ≤ W₀,

G₂ (W) =

C₂ (W – W₀)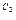, якщо W > W₀,

де С₂ > 0, 0 < C₃ < 1 – коефіцієнти (параметри) функцій попиту та пропозиції.

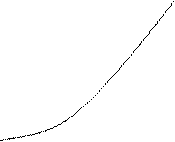
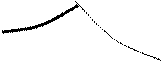
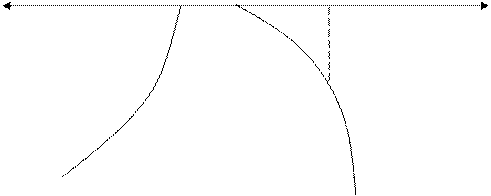
Типові схеми розрахунків за моделлю Хікса-Хансена (рис. 10.1):

i

IS

LM

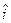
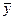W W₀ y^*

y

L^*

L^D

L^S L y = F (L)

Рис. 10.1

І. Знаходимо стан рівноваги (ситуацію повної зайнятості – не плутати з повним використанням вільних трудових ресурсів!) з рівняння

L^* = G ₁ (W) = G₂ (W).

Підставивши L^* до виробничої функції, знайдемо ВВП, що їй відповідає:

y^* = F (L^*).

Порівняємо значення y^* з найбільш досяжним значенням ВВП 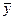за наявних фінансових обмежень. Останнє визначається із співвідношення:

,

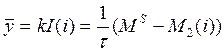йому відповідатиме рівноважна норма відсотку .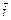

Якщо (як це показано на рис. 10.1) рівноваги на ринку праці не можна досягти за наявних фінансових ресурсів, потрібно змінювати параметри моделі IS-LM (перш за все, M^S та 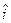), або погодитись на додаткове безробіття.

Якщо 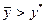- рівновага на ринку праці досягається за рахунок відсутності фінансової рівноваги. При цьому норма проценту має бути у межах [ i ₁, i ₂], де i ₁ – розв’язок рівняння 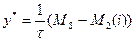, i ₂ - розв’язок рівняння y^* = kI (i).

Якщо 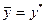, то досягнуто узгодженої фінансової рівноваги та рівноваги на ринку праці.

ІІ. Фіксуємо певне значення ВВП 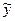(ним, зокрема, може бути 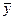- найбільше досяжне значення ВВП). З рівняння

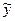= F(L)

визначаємо потребу у трудових ресурсах L. Підставивши це значення до рівняння

L^D = G ₁ (W) = L,

знаходимо відповідний рівень оплати праці .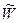

Дата добавления: 2014-01-07