Обратная матрица. Определитель матрицы

Матрица 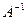называется обратной для матрицы А, если 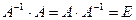, где Е - единичная матрица.

Для квадратной матрицы А обратная матрица существует тогда и только тогда, когда определитель, составленный из элементов прямой матрицы, отличен от нуля, т.е. 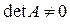. Определители прямой и обратной матриц связаны соотношением: .

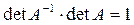Рис. 3.12. Примеры действий с матрицами.

Определитель(детерминант) квадратной матрицы 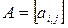- число(обозначение 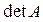), характеризующее свойства матрицы. Вычисление определителя матрицы вручную – трудоёмкий процесс.

В Mathcad имеются две возможности вычисления определителя.

Если элементами матрицы являются числа, то нужно на панели Matrix щёлкнуть мышью знак «Determinant», напечатать в открывшемся шаблоне имя матрицы и напечатать =(равно) для просмотра результата.

В том случае, когда элементами матрицы являются идентификаторы нужно так же ввести шаблон определителя, заполнить его и щёлкнуть мышью символический знак равенства (левая стрелка) на панели Symbolic(символьные вычисления) для отображения результата в символьной форме (рис. 3.12).

3.2.6. Оператор vectorize.

В Mathcad есть один оператор множества называемый оператором векторизации (vectorize), который особенно полезен для многократного выполнения одинаковых вычислений.

Рис. 3.13. Примеры записи оператора векторизации.

Введение этого оператора устраняет противоречие, связанное со скалярным произведением векторов. Сущность этого противоречия состоит в следующем. Если, например, вектор умножается скалярно на число, то получается новый вектор, каждый элемент которого умножен на это число, но если скалярно умножается тот же вектор сам на себя, то результатом будет число, равное сумме квадратов элементов вектора, а не вектор.

Оператор векторизации же, в отличие от скалярного произведения, производит умножение каждого элемента v_k (k=1…n) вектора V на элемент с тем же номером (с тем же индексом) другого или того же вектора, производя новый вектор такой же длины n.

Ввести оператор vectorize можно двумя способами:

- напечатать Ctrl – (минус) «имя первого операнда»[Shift]* «имя второго операнда» = (равно) и щёлкнуть левой кнопкой мыши;

- щёлкнуть мышью опцию «f(M)» на матричной панелиMatrixи выполнить те же действия, что и выше.

Операндами оператора векторизации могут быть и матрицы одинаковой размерности. Например, если напечатать M*M [пробел] [Ctrl] – (минус) = ( равно), то получается новая квадратная матрица той же размерности, элементы которой равны произведению каждого элемента матрицы М на самого себя.

Примечание: Число операндов в операторе vectorize может быть любым, не обязательно равным двум.

Дата добавления: 2014-01-07