Законы механики жидкости и газа

3.1 Уравнение неразрывности и закон сохранения массы

В динамике сплошных сред (жидкостей, газов, упругих и других «твердых» деформируемых тел) задаются непрерывные распределения динамических и, вообще, физических величин по сплошной среде, характеризуемых плотностью распределения этих величин.

Первым примером такого задания может служить плотность распределения массы в виде предела отношения массы малого объема, заключающего в себе данную точку М, к объему, когда последний стремится к нулю, стягиваясь к точке М. Отношение называют средней плотностью в объеме, а предел этого отношения – плотностью среды в данной точке М и обозначают буквой r, так что

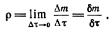(3.1)

Отсюда непосредственно следуют выражения массы элементарного объема через плотность

(3.2)

и массы т выделенного в среде конечного объема

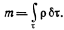(3.3)

В ньютоновской механике масса жидкого, т. е. состоящего во все время движения из одних и тех же частиц, объема, сохраняет постоянную величину, так что, согласно формуле (3.2) (d/dt — символ индивидуальной производной по времени),

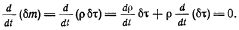(3.4)

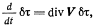
и, следовательно, равенство 3.4) приведется к такому

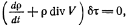
откуда, в силу произвольности величины dt, следует

(3.5)

Уравнение (3.5) обычно называют уравнением сплошности или уравнением неразрывности, хотя, быть может, ему более соответствовало бы наименование уравнения сохранения массы.

Если поле плотности стационарно (dr/dt=0), уравнение неразрывности примет вид

или в проекциях скорости V_k (k=l, 2, 3) (суммирование по k)

В случае постоянной плотности (несжимаемая однородная среда) получим уравнение несжимаемости жидкости

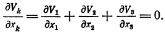или (3.6)

3.2 Закон сохранения энергии и уравнение Бернулли для идеальной жидкости

Индивидуальная производная по времени от полной энергии данного движущегося объема среды равна сумме мощностей приложенных к выделенному объему и его поверхности внешних массовых и поверхностных сил и отнесенного к единице времени количества энергии, подведенной извне к объему. Этот закон выражается интегральным равенством

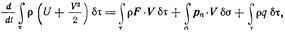(3.7)

где U — удельная (отнесенная к единице массы) внутренняя энергия среды, включающая в себя все возможные виды энергии внутренних движений материи (в задачах механики жидкости и газа — это в первую очередь тепловая энергия), a q—удельное количество энергии, подведенное извне в единицу времени к данной частице среды и заключающее в себе отличные от работы макроскопических механических сил тепловые и нетепловые виды энергии. Сумма внутренней и внешней (кинетической) энергии носит наименование полной энергии.

Простейшей моделью сплошной текучей среды является идеальная среда, обладающая при движении свойством идеальной текучести.

Вдоль траектории или линии тока трехчлен Бернулли В сохраняет одно и то же значение

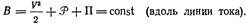(3.8)

Полученное равенство можно рассматривать как первый интеграл уравнения Эйлера, справедливый в случае стационарного движения при наличии функции давления, представляющей потенциал объемного действия поверхностных сил, и потенциала объемных сил. Этот интеграл может трактоваться как интеграл механической энергии уравнения движения центра инерции элементарного объема жидкости (интеграл Бернулли).

Равенство (3.8) выражает следующую теорему Бернулли: при стационарном баротропном движении идеальной жидкости под действием потенциальных объемных сил сумма кинетической энергии единицы массы, функции давления и приведенного к единице массы потенциала объемных сил сохраняет вдоль линии тока (траектории) постоянное значение.

Рассмотрим частные случаи теоремы Бернулли, относящиеся к отдельным простейшим баротропным процессам.

В случае движения несжимаемой жидкости (r=const) имеем

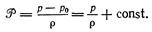
Ограничиваясь среди объемных сил только силами тяжести и направляя вертикальную ось z вверх, получим

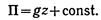
Тогда из (3.8) имеем

(3.9)

или, если перейти от плотности r к удельному весу

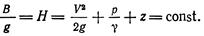(3.10)

Отдельные члены равенства (3.10) имеют размерность длины и называются соответственно скоростной, пьезометрической и (z) нивелирной высотами. Сумма этих высот H называется гидравлической высотой.

Формула (3.10) приводит к классической формулировке теоремы Бернулли: при стационарном движении тяжелой идеальной несжимаемой жидкости гидравлическая высота, равная сумме скоростной, пьезометрической и нивелирной высот, сохраняет постоянное значение вдоль линии тока (траектории) или вихревой линии. Эта форма теоремы Бернулли имеет основное значение в гидравлике и называется уравнением Бернулли.

Предположим в дальнейшем, что объемными силами по сравнению с поверхностными (давлением) можно пренебречь; тогда уравнение Бернулли примет более простой вид

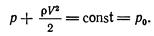(3.11)

Первый член левой части этого равенства называют пьезометрическим напором, второй — скоростным или динамическим напором, сумму их — полным напором р₀. Теорему Бернулли формулируют так: при стационарном движении идеальной несжимаемой жидкости в отсутствие объемных сил полный напор, равный сумме пьезометрического и скоростного напора, сохраняет свою величину вдоль линии тока (траектории) или вихревой линии.

Получим следующие формы теоремы Бернулли:

а) для изотермического движения (Т = const, p/r = p₀/r₀, р/p₀=r/ r₀)

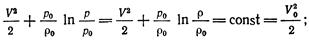(3.12)

б) для адиабатического движения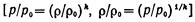

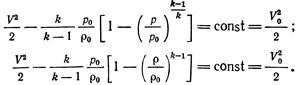(3.13)

Дата добавления: 2014-01-07