Двумерную

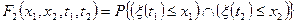
и так далее до произвольной конечномерной функции распределе­ния

.

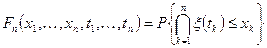Последовательность функций распределения , , 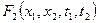представляет своеобразную лестницу, поднимаясь по которой уда­ется все подробнее характеризовать случайный процесс.

Рассматриваемая последовательность функций распределения как функ­ций порогов 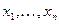должна обладать всеми свойствами функ­ций распределения вероятностей, изложенными в п.1.2. В част­ности, из функций распределения 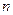-го порядка можно получить все функции распределения более низких порядков, вплоть до первого. Однако в отличие от функций распределения случайных величин, функции распределения случайных процессов зависят не только от порогов 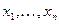, но и от моментов .

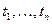Функции распределения случайного процесса должны удовлет­ворять условию симметрии (симметрии по парам аргументов)

,

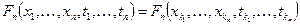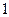где целые числа от до 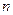, расположенные в произвольном порядке, и условию согласованности

,

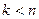
Дата добавления: 2014-01-06