Граничные условия для векторов ЭМП

Граничные условия для векторов ЭМП. Закон сохранения заряда. Теорема Умова-Пойнтинга

Примеры применения MATLAB

Задача 1.

Дано: Внутри объёма тетраэдра магнитная индукция и намагниченность вещества изменяются по линейному закону. Координаты вершин тетраэдра заданы, значения векторов магнитной индукции и намагниченности вещества в вершинах также заданы.

Вычислить плотность электрического тока в объёме тетраэдра, используя m-функцию, составленную при решении задачи в предыдущем параграфе. Вычисление выполнить в командном окне MATLAB, предполагая, что пространственные координаты измеряются в миллиметрах, магнитная индукция – в теслах, напряжённость магнитного поля и намагниченность – в кА/м.

Решение.

Зададим исходные данные в формате, совместимом с m-функцией grad_div_rot:

>> nodes=5*rand(4,3)

nodes =

0.94827 2.7084 4.3001

0.96716 0.75436 4.2683

3.4111 3.4895 2.9678

1.5138 1.8919 2.4828

>> B=rand(4,3)*2.6-1.3

B =

1.0394 0.41659 0.088605

0.83624 -0.41088 0.59049

0.37677 -0.54671 -0.49585

0.82673 -0.4129 0.88009

>> mu0=4e-4*pi % абcолютнаq магнитнаq проницаемоcть вакуума, мкГн/мм

mu0 =

0.0012566

>> M=rand(4,3)*1800-900

M =

122.53 -99.216 822.32

-233.26 350.22 40.663

364.93 218.36 684.26

83.828 530.68 -588.68

>> [grad,div,cur_dens]=grad_div_rot(nodes,ones(4,1),B/mu0-M)

grad =

0 -3.0358e-017 0

div =

-712.01

cur_dens =

-914.2 527.76 -340.67

В данном примере вектор полной плотности тока в рассматриваемом объёме получился равным (-914.2× 1 _x + 527.76× 1 _y – 340.67× 1 _z) А/мм². Чтобы определить модуль плотности тока, выполним следующий оператор:

>> cur_d=sqrt(cur_dens*cur_dens.')

cur_d =

1109.2

Вычисленное значение плотности тока не может быть получено в сильно намагниченных средах в реальных технических устройствах. Данный пример – чисто учебный. А теперь проверим корректность задания распределения магнитной индукции в объёме тетраэдра. Для этого выполним следующий оператор:

>> [grad,div,cur_dens]=grad_div_rot(nodes,ones(4,1),B)

grad =

0 -3.0358e-017 0

div =

-0.34415

cur_dens =

-0.38115 0.37114 -0.55567

Здесь мы получили значение div B = -0.34415 Тл/мм, чего не может быть в соответствии с законом непрерывности линий магнитной индукции в дифференциальной форме. Из этого следует, что распределение магнитной индукции в объёме тетраэдра задано некорректно.

Задача 2.

Пусть тетраэдр, координаты вершин которого заданы, находится в воздухе (единицы измерения – метры). Пусть заданы значения вектора напряжённости электрического поля в его вершинах (единицы измерения – кВ/м).

Требуется вычислить объёмную плотность электрического заряда внутри тетраэдра.

Решение можно выполнить аналогично:

>> nodes=3*rand(4,3)

nodes =

2.9392 2.2119 0.59741

0.81434 0.40956 0.89617

0.75699 0.03527 1.9843

2.6272 2.6817 0.85323

>> eps0=8.854e-3 % абсолютная диэлектрическая проницаемость вакуума, нФ/м

eps0 =

0.008854

>> E=20*rand(4,3)

E =

9.3845 8.4699 4.519

1.2956 10.31 11.596

19.767 6.679 15.207

11.656 8.6581 10.596

>> [grad,dens_z,rot]=grad_div_rot(nodes,ones(4,1),E*eps0)

grad =

2.2204e-016 0 0

dens_z =

0.10685

rot =

0.076467 0.21709 -0.015323

В данном примере объёмная плотность заряда получилась равной 0.10685 мкКл/м³.

Пусть некоторая поверхность S разделяет среды 1 и 2 (рис. 2).

Рис. 2.

Рассмотрим некоторую точку на этой поверхности. Вектор единичной нормали к поверхности S в этой точке направлен из среды 1 в среду 2. Тогда поведение векторов H, B, E, D в этой точке, в соответствии с уравнениями Максвелла описываются следующим образом

,

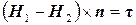где 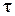– поверхностная плотность тока, А/м.

Если 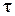= 0, то H _{1 t} – H _{2 t} = 0.

.

Если E _{2c t} – E _{1c t} = 0, то E _{2 t} – E _{1 t} = 0

, т. е.

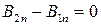
или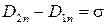

Здесь обозначено: H ₁ – вектор напряжённости магнитного поля на поверхности раздела сред в среде №1; H ₂ – то же в среде №2; H _{1 t} – тангенциальная (касательная) составляющая вектора напряжённости магнитного поля на поверхности раздела сред в среде №1; H _{2 t} – то же в среде №2; E ₁ вектор полной напряжённости электрического поля на поверхности раздела сред в среде №1; E ₂ – то же в среде №2; E _1c – сторонняя составляющая вектора напряжённости электрического поля на поверхности раздела сред в среде №1; E _2с – то же в среде №2; E _{1 t} – тангенциальная составляющая вектора напряжённости электрического поля на поверхности раздела сред в среде №1; E _{2 t} – то же в среде №2; E _{1с t} – тангенциальная сторонняя составляющая вектора напряжённости электрического поля на поверхности раздела сред в среде №1; E _{2 t} – то же в среде №2; B ₁ – вектор магнитной индукции на поверхности раздела сред в среде №1; B ₂ – то же в среде №2; B _{1 n} – нормальная составляющая вектора магнитной индукции на поверхности раздела сред в среде №1; B _{2 n} – то же в среде №2; D ₁ – вектор электрического смещения на поверхности раздела сред в среде №1; D ₂ – то же в среде №2; D _{1 n} – нормальная составляющая вектора электрического смещения на поверхности раздела сред в среде №1; D _{2 n} – то же в среде №2; σ – поверхностная плотность электрического заряда на границе раздела сред, измеряемая в Кл/м².

Дата добавления: 2014-01-07