Пространственные интегральные уравнения в магнитостатике

Распределение напряженности магнитного поля в вакууме, вызванное совместным действием электрических токов и объемно распределенных магнитных диполей определяется следующим интегральным соотношением

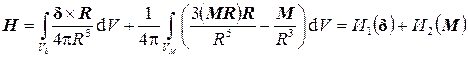
Магнитные свойства вещества могут описываться характеристиками M = f(H), поэтому пространственное интегральное уравнение магнитостатики имеет вид

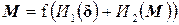(3)

Уравнение (3) решается относительно вектора намагниченности, поэтому расчетной областью при его решении является объем V_M, занятый ферромагнитными материалами. Вычислительные методы, основанные на решении уравнения (3), называются методами пространственных интегральных уравнений (ПрИУ). Во многих случаях эти методы оказываются более экономичными, чем дифференциальные методы, основанные на уравнении (1) или на векторном уравнении магнитостатики.

Дата добавления: 2014-01-07