Частотные характеристики (ЧХ) динамической системы

Динамическая система описывается дифференциальным уравнением:

(7.1)

вынужденная составляющая реакции 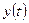на входящее воздействие 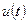называется установившейся реакцией .

Если система устойчива, то (7.2)

Найти можно по формуле:

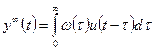(7.3)

Пример:

Пусть входное воздействие гармоническое, а дифференциальное уравнение имеет вид

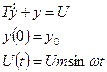
Решение:

(*)

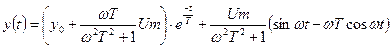Из (*) получаем

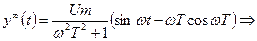
причём

Вывод: установившаяся реакция системы на гармоническое воздействие 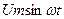есть гармоническая функция той же частоты . Аналогично реакция на есть 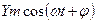, поэтому установившаяся реакция на воздействие есть .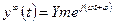

Теорема 7.1. Если система устойчива в смысле выполнения неравенства

(7.4)

где то установившаяся реакция на гармоническое воздействие есть гармоническая функция той же частоты но в общем случае другой амплитуды с фазовым сдвигом относительно входной функции, причём

(7.5)

а (7.6)

Доказательство:

(7.7)

Поскольку 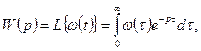то выражение [в (7.7)]

есть (оно представляет собой преобразование Фурье функции : ).

Поскольку 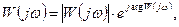то (7.7) принимает вид:

отсюда 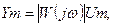что и требовалось доказать.

Функция 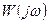называется частотной передаточной функцией (ЧПФ). Другие частотные характеристики:

АЧХ

ФЧХ

ВЧХ

МЧХ

Дата добавления: 2014-01-07