
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение фазы по ЛАХ минимально-фазовой системы
|
|
|
|
Теоретически связь между ЛАХ и ЛФХ выражается формулой:
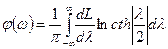 (11.1)
(11.1)
где 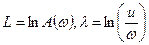 ;
;  вспомогательная переменная (круговая частота).
вспомогательная переменная (круговая частота).
Согласно (11.1) 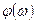 есть взвешенная сумма коэффициентов наклона ЛАХ, причём роль весового множителя выполняет функция
есть взвешенная сумма коэффициентов наклона ЛАХ, причём роль весового множителя выполняет функция 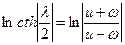 .
.
Из формулы (11.1) и графика следует, что на значение ЛФХ на данной частоте 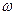 наибольшее влияние оказывают значения коэффициентов наклона ЛАХ в окрестности этой частоты, т.к. именно здесь весовой множитель максимален.
наибольшее влияние оказывают значения коэффициентов наклона ЛАХ в окрестности этой частоты, т.к. именно здесь весовой множитель максимален.
Формула (11.1) не пригодна для практического использования в виду громоздкости. Для точного определения ЛФХ можно по ЛАХ записать передаточную функцию, а по ней с помощью ЭВМ построить ЛФХ. Для приближенного (эскизного) построения ЛФХ можно представить ЛАХ в виде произведения сомножителей вида: 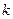 ,
, 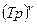 и
и 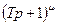 , где
, где 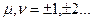 . Мы говорим о ЛАХ не имеющих резонансных всплесков и провалов, после чего для каждого сомножителя изобразить соответствующую ЛФХ и получить результирующую ЛФХ их сложением. Однако существует простой приближенный способ определения фазы по ЛАХ минимально фазовой системы произвольного вида, не имеющей резонансных всплесков:
. Мы говорим о ЛАХ не имеющих резонансных всплесков и провалов, после чего для каждого сомножителя изобразить соответствующую ЛФХ и получить результирующую ЛФХ их сложением. Однако существует простой приближенный способ определения фазы по ЛАХ минимально фазовой системы произвольного вида, не имеющей резонансных всплесков: 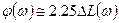 (11.2)
(11.2)
где  перепад (дБ) на интервале шириной две декады с рассматриваемой частотой
перепад (дБ) на интервале шириной две декады с рассматриваемой частотой 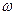 по середине.
по середине.
Обоснование: ЛАХ произвольного вида без резонансных всплесков всегда может быть представлена как сумма ЛАХ типовых звеньев с передаточными функциями: 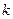 ,
, 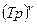 и
и 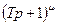 , где
, где 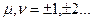 . Для
. Для 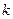 и
и 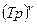 формула (11.2) является точной, а для
формула (11.2) является точной, а для 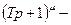 приближенная с максимальной погрешностью
приближенная с максимальной погрешностью 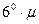 . Поэтому в силу линейности и справедливости принципа суперпозиции формула (11.2) справедлива для произвольной ЛАХ.
. Поэтому в силу линейности и справедливости принципа суперпозиции формула (11.2) справедлива для произвольной ЛАХ.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 432; Нарушение авторских прав?; Мы поможем в написании вашей работы!