Управляемая каноническая форма

При различном выборе переменных состояния получаются различные уравнения в форме переменных состояния.

Пусть 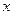и векторы состояния в двух различных базисах одного и того же линейного пространства. При этом они связаны не особенным преобразованием.

(19.1)

неособенная матрица.

Найдем связь между матрицами для обоих описаний. Подставим 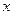из (19.1) в (19.2).

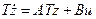
(19.6)

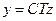(19.7)

Сравнивая (19.6) и (19.7) с (19.4) и(19.5) получаем:

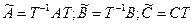(19.8)

Отсюда:

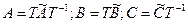(19.9)

Преобразования вида преобразования подобных. С его помощью получать различные специальные (канонические) формы матриц и уравнений.

Например:

Если 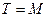, где , а собственный вектор матрицы 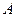соответствующий собственному значению (здесь говорим о случае, когда все попарно различные, т.е. простые), то .

Рассмотрим УКФ, она характеризуется следующим видом матрицы системы:

(19.10)

где 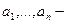коэффициенты приведенного характеристического полинома.

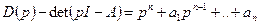(19.11)

Рассмотрим получение УКФ по ПФ системы с одним входом и одним выходом.

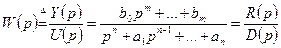(19.12)

I. 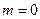, т.е.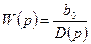

Для получения УКФ в качестве переменных состояния выбирают выходную переменную и все ее производные до включительно.

(19.13)

Таким образом (19.14)

Поэтому из (19.13) сразу получаются все уравнения состояния кроме последнего (смотри (19.14)), а также уравнение выхода 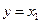(19.15)

Последнее уравнение состояния получаем из передаточной функции переходом во временную область.

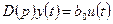
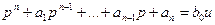
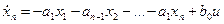(19.16)

На основании (19.14. … 19.16) получаем

где матрица 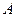имеет форму (19.10), а матрицы и таковы:

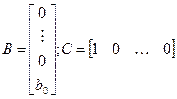(19.17)

Уравнениям УКФ соответствует структурная схема.

II. Передаточная функция (19.12).

В этом случае выбирать в качестве переменных состояния нельзя, поскольку в последнем уравнении состояния появится производная от входного воздействия благодаря числителю ПФ.

Поэтому для получения УКФ поступают следующим образом: Поступают, что по аналогии с (19.14) первые 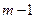уравнения имеют вид:

(19.18)

Кроме того 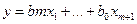(19.19)

В этом случае последнее уравнение состояния примет вид:

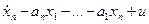(19.20)

Тогда матрица 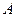имеет прежний вид (19.10), а и таковы:

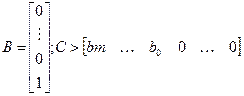(19.21)

Анализ и синтез САУ.

Дата добавления: 2014-01-07