Модальное управление

Рассмотрим систему с одним входом:

(27.1)

Её динамические свойства определяются в основном матрицей 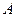(собственные значения 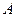– корни ХП). Матрица влияет в меньшей степени (от неё зависят нули ПФ).

Пусть динамика системы (27.1), которую мы назовем объектом – неудовлетворенна. Для придания системе желаемой динамики, охватим объект линейной обратной связью по вектору состояния (ЛОСС).

Закон управления:

(27.2)

где 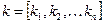– матрица обратной связи;

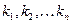– коэффициенты обратных связей по переменным состояния.

Объединяя (27.1) и (27.2) получим уравнения системы с модальными регуляторами:

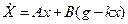
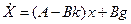(27.3)

Динамические свойства этой системы определяются матрицей:

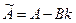(27.4)

Задача модального уравнения: так назначить матрицу 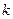, чтобы собственные значения матрицы приобрели требуемые значения. ЛОСС используемая для назначения собственных значений матрицы системы называется модальным регулятором.

Теорема 27.1. Выбором матрицы 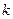собственных значений матрицы могут быть помещены в любые наперед заданные точки комплексной плоскости (с ограничением, что комплексные числа образуют сопряженные пары) или, что то же самое, характеристический полином может быть равным произвольному приведенному полиному с вещественными коэффициентами, тогда и только тогда, когда пара матриц полностью управляема.

Замечание 1: говорят, что пара матриц полностью управляема, если система (27.1) – полностью управляема.

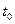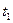Замечание 2: система (27.1) является полностью управляемой, если она может быть переведена из произвольного начального состояния , в момент времени , в произвольное конечное состояние , в момент времени , за ограниченный промежуток времени , при помощи ограниченного управления 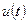, определенного на интервале .

Замечание 3: система (27.1) полностью управляема тогда и только тогда, когда ранг матрицы управляемости 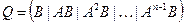(27.5)

равен порядку системы: 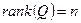(27.6)

Дата добавления: 2014-01-07