
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Более компактная (универсальная) запись различных моделей
Для того чтобы сделать модель более компактной используют оператор сдвига (lag operator).
Обозначение оператора сдвига — 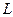 .
.
Запись 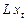 означает сдвиг
означает сдвиг 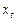 на один период назад:
на один период назад:
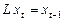 .
.
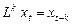 — эта запись означает применение оператора сдвига к объясняющей переменной
— эта запись означает применение оператора сдвига к объясняющей переменной 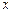 в момент времени
в момент времени 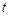
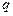 раз, то есть переменная
раз, то есть переменная 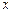 от момента времени
от момента времени 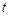 сдвигается влево (назад) на
сдвигается влево (назад) на 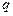 лагов.
лагов.
Пример:
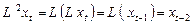 .
.
Введем обозначение полиномов оператора сдвига:
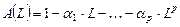 , где
, где 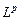 означает, что оператор
означает, что оператор 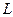 применен
применен 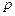 раз;
раз;
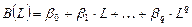 — для DL моделей;
— для DL моделей;
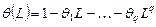 , где
, где 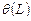 — оператор, применяемый к остаткам;
— оператор, применяемый к остаткам;
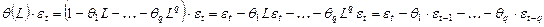 .
.
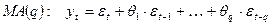 — запись «Moving Average» (скользящая средняя).
— запись «Moving Average» (скользящая средняя).
Упражнение. Получить полином оператора сдвига 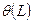 для следующей спецификации MA(q):
для следующей спецификации MA(q):
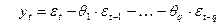 .
.
Имеет ли значение знак перед коэффициентом 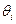 в спецификации MA(q) и почему?
в спецификации MA(q) и почему?
В общем виде, с использованием операторов полиномов, любая модель временных рядов может быть записана следующим образом:
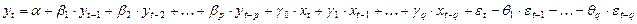 ,
,
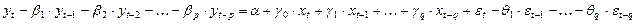 ,
,
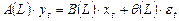 .
.
Если в спецификации модели (конкретной формуле) присутствует только запись 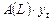 , то это означает, что модели относятся к классу AR.
, то это означает, что модели относятся к классу AR.
Если в спецификации модели (конкретной формуле) присутствует только запись 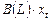 , то это означает, что модели относятся к классу DL.
, то это означает, что модели относятся к классу DL.
Если в спецификации модели (конкретной формуле) присутствует только запись 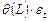 , то это означает, что модели относятся к классу MA.
, то это означает, что модели относятся к классу MA.
Задача:
Используя регрессионный аппарат построить зависимость для прогнозирования объема реализации на основе данных о динамике этого показателя (данные в условных единицах):
17, 16, 21, 24, 23, 26, 28.
Дано уравнение регрессии вида
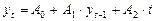 .
.
В данном примере построена модель временного ряда с использованием зависимости от времени (t).
Для нахождения коэффициентов регрессии поставим задачу МНК:
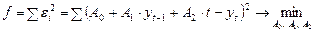 ,
,
Необходимые условия экстремума:
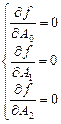 ,
,
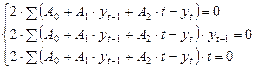 ,
,
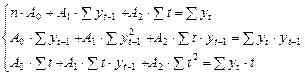 .
.
Построим таблицу и рассчитаем в ней все необходимые коэффициенты.
| 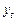
| 
| 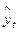
| 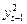
| 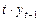
| 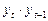
| 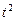
| 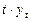
|
| 17,43662 | ||||||||
| 2,10387 | ||||||||
| -0,36444 | ||||||||
| 0,00000 | ||||||||
| 0,00000 | ||||||||
| 0,00000 | ||||||||
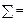 21 21
| 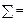 138 138
| 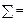 127 127
| 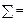 19,176 19,176
| 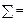 2767 2767
| 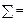 479 479
| 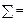 2990 2990
| 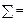 91 91
| 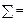 520 520
|
Получим систему уравнений:
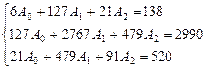 .
.
Решим данную систему методом Гаусса и получим значения искомых коэффициентов для уравнения регрессии:
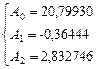 .
.
Таким образом, уравнение регрессии примет вид:
 .
.
Результат можно проверить, построив модель в пакете Statistica 6.0.
Для проверки качества модели рассчитывается следующий коэффициент:
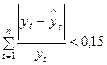
Если его значение меньше 15%, то уравнение можно использовать в целях прогнозирования.
|
|
Дата добавления: 2014-01-06; Просмотров: 583; Нарушение авторских прав?; Мы поможем в написании вашей работы!