Лекция 6. Дифференциальные уравнения движения

Вопросы для самопроверки

1. По каким признакам установившееся движение жидкости отличается от неустановившегося, равномерное от неравномерного, напорное от безнапорного? 2. Чем отличается траектория частицы жидкости от линии тока? Когда траектория и линия тока совпа­дают? 3. Что называется расчетной моделью потока? 4. Можно ли измерить скорость струйки? Можно ли измерить среднюю ско­рость потока? 5. Что учитывается гидравлическим радиусом? 6. Каков геометрический смысл различных членов уравнения Бернулли? Каков их энергетический смысл?

Уравнения неразрывности. Уравнения Бернулли для идеальной и реальной жидкостей и его интерпретация. Графическое изображение уравнения Бернулли. Гидравлический и пьезометрический уклоны.

Основное содержание лекции

Основным уравнением гидродинамики, применяемым в гидравлических расчетах потока реальной жидкости при установившемся движении, является уравнение Бернулли:

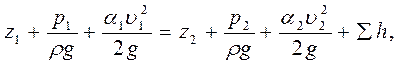
где z - геометрический напор - возвышение центра тяжести живого сечения над произвольно выбранной горизонтальной плоскостью сравнения (в энергетическом отношении — это удельная, отнесенная к единице веса жидкости, энергия положения); 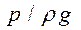- пьезометрический напор, т. е. превышение уровня жидкости в пьезометре над точкой, аппликата которой z (удельная энергия давления); 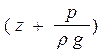- превышение уровня жидкости в пьезометре над плоскостью сравнения (удельная потенциальная энергия); 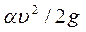- скоростной напор (удельная кинетическая энергия); 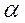- коэффициент неравномерности распределения скоростей по сечению потока (коэффициент Кориолиса), отношение истинной кинетической энергии потока к кинетической энергии, определенной по средней скорости 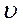; 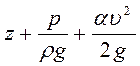- удельная механическая энергия; 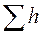- количество удельной механической энергии, которую жидкость теряет при преодолении гидравлических сопротивлений на пути между сечениями 1 и 2. Эта часть механической энергии в результате работы сил трения переходит в тепловую энергию и рассеивается в пространстве. Эти потери механической энергии называются гидравлическими потерями. Они состоят из местных гидравлических потерь 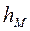и гидравлических потерь по трению :

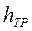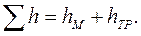
Физический смысл уравнения Бернулли: при установившемся движении жидкости сумма трех удельных энергий остается неизменной вдоль потока и равной общему запасу удельной энергии. Уравнение Бернулли можно выразить и в следующем виде, где все члены представляют собой энергию, отнесенную к единице объема

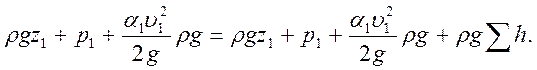
При решении практических задач для установившегося движения несжимаемой жидкости вместе с уравнением Бернулли применяется и уравнение постоянства расхода, т. е. равенства расхода во всех сечениях установившегося потока:

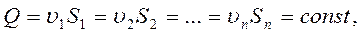
где 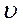- средняя скорость в живом сечении потока; S - площадь живого сечения.

При решении практических задач целесообразно руководствоваться следующим:

уравнения Бернулли, а также уравнение постоянства расхода применяются лишь для установившегося движения вязкой несжимаемой жидкости. Движение жидкости между расчетными сечениями должно быть параллельно-струйным или плавно изменяющимся;

уравнение Бернулли составляется для двух живых сечений, нормальных к направлению скорости. Эти сечения должны располагаться на прямолинейных участках потока;

одно из расчетных сечений необходимо брать там, где требуется определить давление р, геометрический напор z. или скорость 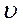, второе, где z, р и 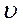известны;

нумеровать расчетные сечения следует так, чтобы жидкость двигалась от 1 ко 2 сечению. B противном случае, меняется знак потерь напора;

плоскость сравнения должна быть горизонтальной. Bысота положения центра тяжести живого сечения z выше плоскости сравнения считается положительной, а ниже - отрицательной;

последний член уравнения учитывает все потери напора между расчетными сечениями как местные, так и потери на трение;

если в уравнении Бернулли имеется ряд неизвестных скоростей, то к нему дополнительно дописывается столько уравнений постоянства расхода, сколько есть неизвестных скоростей, После этого все скорости выражаются через одну скорость, которая уже рассчитывается по написанному уравнению Бернулли.

Дата добавления: 2014-01-07