Пример модификации фильтра МНК 2-го порядка

Передаточная функция: выражение (2.1.7). Частотная характеристика (нормировку можно снять):

H(w) = -3exp(2jw)+12exp(jw)+17+12exp(-jw)-3exp(-2jw).

Замена концевых коэффициентов {значение 3} на параметр b и упрощение:

H(w) = 17+24 cos(w)+2b cos(2w).

При w = p: H(p) = 17-24+2b = 0. Отсюда: b = 3.5

Новая частотная характеристика (с приведением коэффициентов к целым числам):

H(w) = 68+96 cos(w)+14 cos(2w). Сумма коэффициентов при w = 0: H(0) = 68+96+14 = 178.

Нормированная частотная характеристика: H(w) = (68+96 cos(w)+14 cos(2w))/178.

Коэффициенты фильтра: h_n = {(7,48,68,48,7)/178}.

Пример- задание: Модифицировать 7, 9 и 11-ти точечные сглаживающие фильтры МНК 2-го порядка.

Контроль: ⁷h_n = {(1,6,12,14,12,6,1)/52}. ⁹h_n = {(-1,28,78,108,118,108,78,28,-1)/548}.

¹¹h _n = {(-11,18,88,138,168,178,168,138,88,18,-11)/980}.

Сравнительные графики частотных характеристик модифицированных фильтров МНК второго порядка приведены на рисунке 2.1.8.

Фильтры МНК третьего порядка по своим частотным характеристикам эквивалентны фильтрам второго порядка.

Фильтры МНК 4-го порядка. Расчет по аналогичной методике сглаживающих фильтров МНК 4-ой степени дает следующие результаты:

h_0-3 = (131,75,-30,5)/231,

h_0-4 = (179,135,30,-55,15)/429,

h_0-5 = (143,120,60,-10,-45,18)/429,

h_0-6 = (677,600,390,110,-135,-198,110)/2431.

На рис. 2.1.12 приведено сопоставление частотных характеристик одноразмерных фильтров МНК 1-го, 2-го и 4-го порядка.

В целом, по сглаживающим фильтрам МНК можно сделать следующие выводы:

1. Повышение порядка фильтра увеличивает степень касания частотной характеристикой уровня коэффициента передачи Н=1 на частоте w = 0 и расширяет полосу пропускания фильтра.

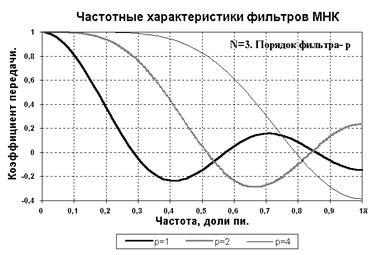Рис. 2.1.12. Сглаживающие фильтры МНК.

2. Увеличение количества членов фильтра приводит к сужению полосы пропускания и увеличивает крутизну ее среза.

3. Модификация фильтров уменьшает осцилляции передаточной функции в полосе подавления сигналов.

Совместное изменение этих параметров позволяет подбирать для сглаживания данных такой фильтр МНК, частотная характеристика которого наилучшим образом удовлетворяет частотному спектру сигналов при минимальном количестве коэффициентов фильтра.

Дата добавления: 2014-01-07