Способы генерации ключей

Поскольку стойкость шифра определяется секретностью ключа, то вскрытию мо­жет подвергнуться не сам шифр, а алгоритм генерации ключей. Иными словами, если для генерации ключей используется нестойкий алгоритм, криптосистема будет нестой­кой.

Длина ключа в DES-алгоритме составляет 56 бит. Вообще говоря, в качестве клю­ча можно использовать любой 56-битный вектор. На практике это правило часто не соблюдается. Например, широко распространенная программа шифрования файлов Norton Discreet, входящая в пакет Norton Utilities (версии 8.0 или более младшей вер­сии), которая предназначена для работы в операционной системе DOS, предлагает пользователю программную реализацию DES-алгоритма. Однако при вводе ключа раз­решается подавать на вход программы только те символы, старший бит представле­ния которых в коде ASCII равен нулю. Более того, пятый бит в каждом байте введен­ного ключа является отрицанием шестого бита, и в нем игнорируется младший бит. Это означает, что мощность ключевого пространства сокращается до 240 ключей. Та­ким образом, программа Norton Discreet реализует алгоритм шифрования, ослаблен­ный в десятки тысяч раз по сравнению с настоящим DES-алгоритмом.

В табл. 4.9 приведено количество возможных ключей в зависимости от различных ограничений на символы, которые могут входить в ключевую последовательность, а также указано время, необходимое для проведения атаки методом тотального перебо­ра, при условии, что перебор ведется со скоростью 1 млн ключей в секунду.

Из табл. 4.9 следует, что при переборе 1 млн ключей в секунду можно в приемле­мые сроки вскрывать 8-байтовые ключи из строчных букв и цифр, 7-байтовые буквен-но-цифровые ключи, 6-байтовые ключи, составленные из печатаемых ASCII-симво­лов, и 5-байтовые ключи, в которые могут входить любые ASCII-символы. А если учесть, что вычислительная мощность компьютеров увеличивается вдвое за 1,5 года, то для успешного отражения атаки методом тотального перебора в течение ближай­шего десятилетия необходимо заблаговременно позаботиться о том, чтобы использу­емый ключ был достаточно длинным.

Когда отправитель сам выбирает ключ, с помощью которого он шифрует свои со­общения, его выбор обычно оставляет желать лучшего. Например, некий Петр Серге­евич Иванов скорее предпочтет использовать в качестве ключа Ivanov, чем такую пос­ледовательность символов, как &h>7)g\*. И вовсе не потому, что он принципиально не желает соблюдать элементарные правила безопасности. Просто свою фамилию Ива-

Таблица 4.9. Количество возможных ключей в зависимости от ограничений на символы
\ ключевой последовательности

\ Используемые символы 9 f i ]	Длина символов ключевой последовательности, байт
			7	а
Количество возможных ключей	Время полного перебора	Количество возможных ключей	Время полного переборз	Количество возможных ключей	Время полного перебора	Количество возможных ключей	Время ПОЛНОГО перебора	Количество возможных ключей	Время полного перебора
Строчные буквы (26)	4,7x1 0^5	0,6с	1,3x1 0^7	13с	3,2x10*	6 мин	8, 1x1 0^е	2,3 час	2,2x10"	2,5 ДН
Строчные буквы и цифры (36)	1,8x10*	1,8с	6,1x1 0^7	2 мин	2,3x1 0^9	37 мин	7,9x1 0^10	23 час	2.9x1 0^12	34 дн.
Буквы и цифры (62)	1,6x1 0^7	16с	9,3x10"	16 мин	5,8x1 0^10	17 час	3,6x1 0^1'	42 дн.	2,3x1 0^14	7,0 лет
Печатаемые символы (95)	8,2x1 0^7	1,5 мин	7,8x1 0^е	2,2 час	7,5x1 0^1'	8,6 дн.	7.1хЮ^13	2,3 лет	6,7x1 0^15	21 1 лет
Все ASCII-символы	4,4x1 0^9	1,3 час	1,2х10^10	14дн.	2,9хЮ^14	9,0 лет	7,3х10^1в	2400 лет	1,9х10^19	590000 лет

нов помнит гораздо лучше, чем абракадабру из восьми произвольно взятых символов. Однако при использовании такого ключа сохранить свою переписку в тайне ему не поможет и самый стойкий алгоритм шифрования в мире, особенно если ключи совпа­дают с именами ближайших родственников и записывает он эти ключи на клочках бумаги, которые наклеивает на компьютер. В ходе хорошо организованной атаки ме­тодом тотального перебора квалифицированный криптоаналитик не будет применять все ключи последовательно, один за другим. Он сначала проверит те из них, которые хоть что-то значат для Иванова. Такая разновидность атаки методом тотального пере­бора называется словарной атакой, поскольку противник использует словарь наибо­лее вероятных ключей. В этот словарь обычно входят:

Q Имя, фамилия, отчество, инициалы, год рождения и другая личная информация, имеющая отношение к данному человеку. Например, при словарной атаке против Петра Сергеевича Иванова в первую очередь следует проверить PSI. PSIPSI, PIVANOV, Pivanov, psivanov, peteri, petel, IvanovP, peterivanov, Peter-Ivanov и т. д. Q Словарная база данных, составленная из имен людей, героев мультфильмов и мифи­ческих животных, ругательств, чисел (как цифрами, так и прописью), названий худо­жественных фильмов, научно-фантастических романов, астероидов, планет и цветов радуги, общепринятых сокращений и т. д. В общей сложности для одного конкретно­го человека такая база данных насчитывает более 60 тыс. словарных единиц. Q Слова, которые получены путем внесения различных изменений в словарную базу данных, составленную на предыдущем этапе. Сюда относятся обратный порядок написания слова, замена в нем латинских букв о, 1, z, s на цифры 0,1,2 и 5 соответственно, слова во множественном числе и т. д. Это дает дополни­тельно еще около миллиона словарных единиц для использования в качестве возможного ключа к шифру.

Q Слова, полученные с помощью замены строчных букв на заглавные. Например, вместе со словом Ivanov будут проверяться слова iVanov, ivAnov, ivaNov, ivanOv, ivanoV, IVanov, IvAnov, IvaNov, IvanOv, IvanoV'li т. д. Однако вычислительная мощь современных компьютеров позволяет проверять только одно-, двух- р трех­буквенные замены строчных букв на заглавные.

О Слова на различных иностранных языках. Хотя компьютерные пользователи, в основном, работают с англоязычными операционными системами (DOS, UNIX, Windows и др.), существуют локализованные версии распространенныхрпераци-онных систем, в которых допускается использование другого языка. Это означа­ет, что в качестве ключа на вход программы шифрования может быть подана лю­бая фраза на родном языке ее пользователя. Следует также учитывать, что ключ может быть транслитерирован с любого языка (например, с русского или китайс­кого) на английский и затем в таком виде введен в программу шифрования. LJ Пары слов. Поскольку количество вероятных пар слов, из которых может состо­ять криптографический ключ, слишком велико, на практике криптоаналитики обычно ограничиваются словами из трех и четырех букв.

Поэтому, если все же требуется сохранить ключ в памяти, а запомнить выражение (например, 36f9 67a3 f9cb d931) трудно, тогда для генерации ключа можно использо­вать правила, которые очевидны для вас, но не для постороннего:

О Составьте ключ из нескольких слов, разделенных знаками препинания. Напри­мер, легко запоминаются ключи типа Yankee! Go home.

LI Используйте в качестве ключа сочетание букв, которые представляют собой ак­роним более длинного слова. К примеру, отбросив гласные буквы в предыду­щем выражении, можно сгенерировать ключ Ynk! G hm.

Более привлекателен подход, при котором вместо отдельного слова используется достаточно длинное, легко запоминающееся предложение на русском, английском или другом языке. Такое выражение в криптографии называется паролем. Для преобразо­вания пароля в псевдослучайный битовый ключ можно применить любую однонаправ­ленную хэш-функцию.

Пароль следует выбирать достаточно длинным, чтобы полученный в результате его преобразования ключ был случайным. Известно, что в предложении на английс­ком языке каждая буква содержит примерно 1,3 бита информации. Тогда, чтобы полу­чить 64-битный ключ, пароль должен состоять примерно из 49 букв, что соответству­ет английской фразе из 10 слов.

Пароль должен быть составлен так, чтобы его было легко вспоминать, и в то же время он должен быть достаточно уникальным. Цитата из высказываний Козьмы Прут­кова, которая у всех на слуху, вряд ли подойдет, поскольку его сочинения имеются в форме, доступной для воспроизведения на компьютере, и, следовательно, могут быть использованы в словарной атаке. Лучше воспользоваться творчеством малоизвестно­го поэта или драматурга, процитировав его с ошибками. Эффект будет сильнее, если в цитате, использованной для генерации ключа, присутствуют иностранные слова. Иде­ально подходят для этой цели незатейливые ругательства — их не придется записы­вать, чтобы запомнить. Достаточно стукнуть по пальцу молотком, и пароль автомати­чески придет вам в голову. Надо только сдержаться и не произнести его вслух, чтобы не подслушали посторонние.

Несмотря на все сказанное, залогом наилучшей защиты служит не шаманство при выборе пароля, а случайность полученного ключа. Хороший ключ — это случайный ключ, а значит, заранее будьте готовы к тому, что запомнить его наизусть очень труд-

но. Поскольку в компьютерах используется исключительно цифровая информация, то далее мы будем предполагать, что сообщение, которое мы хотим криптографически преобразовать, переводится в последовательность двоичных цифр. Любая информа­ция (письма, музыка или телевизионный сигнал) может быть представлена в двоичном коде.

Надежный ключ представляет собой случайный битовый вектор. К примеру, если он имеет |щину 56 бит, это значит, что в процессе его генерации с одинаковой вероят­ностью м^>жет получиться любой из 256 возможных ключей. Источником случайных ключей обычно служит природный случайный генератор. Кроме того* источником случайного ключа может быть криптографически надежный генератор псевдослучай­ных двоичных последовательностей. Лучше, чтобы процесс генерации ключей был автоматизирован.

Использовать хороший генератор случайных чисел является очень важно, однако не следует слишком долго спорить о том, какой из генераторов лучше. Важнее приме­нять стойкие алгоритмы шифрования и надежные процедуры работы с ключами.

Во всех алгоритмах шифрования имеются так называемые нестойкие ключи. Это означает, что некоторые из ключей к шифру менее надежны, чем остальные. Поэтому при генерации ключей нужно автоматически проверять их на стойкость и генериро­вать новые вместо тех, которые эту проверку не прошли. К примеру, в DES-алгоритме имеются всего 24 нестойких ключа из общего количества 256, и, следовательно, веро­ятность найти нестойкий ключ пренебрежимо мала. Кроме того, откуда криптоанали-тику знать, что для зашифрования конкретного сообщения или файла был применен именно нестойкий ключ? А сознательный отказ от использования нестойких ключей дает противнику дополнительную информацию о вашей криптосистеме, что весьма нежелательно. С другой стороны, проверить ключи на нестойкость достаточно про­сто, чтобы этим пренебрегать.

Генерировать открытые ключи сложнее, чем секретные, поскольку открытые клю­чи должны обладать определенными свойствами (например, произведением двух про­стых чисел).

Рассмотрим подробнее процесс формирования различных ключей. Чтобы услож­нить шифр, используется не одна-единственная таблица, с помощью которой можно по некоторому правилу переставить буквы или цифры исходного сообщения, а не­сколько таблиц в определенном порядке. Этот порядок и образует ключ шифрования. Если мы используем только две таблицы, обозначенные как «ключ 0» и «ключ 1», то типовым ключом может быть, например, 1101101. В связи с тем, что таблиц несколь­ко, теперь мы будем иметь дело с многоалфавитной подстановкой. И таких таблиц теоретически может быть сколь угодно много. Относительно этого нового источника сложности в шифре возникает вопрос: можно ли упростить таблицы подстановок, сде­лав их меньше? Конечно же, да. Простейшая двоичная подстановка, которую только можно выполнить, — это замена одной двоичной цифры на другую. В этом случае существует всего две различные таблицы подстановок. Рассмотрим их. При этом каж­дая таблица будет соответствовать одному из двух основных типов ключа, как показа­но на рис. 4.22.

Мы предположим, что таблица, помеченная «Ключ 1», заменяет нули сообщения на единицы и, наоборот, таблица, помеченная «Ключ Оз?, оставляет все цифры сообще-

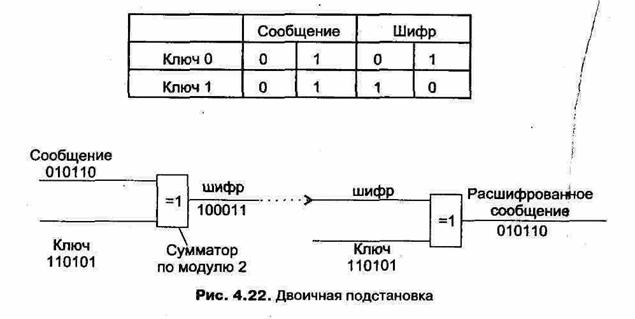
ния неизменными. Оказывается, что тот же самый эффект можно получить с помощью сложения по модулю 2: две одинаковые цифры в результате такой операции дают О, две различные — 1. Поэтому в рассматриваемом случае шаблонный ключ можно на­звать также аддитивным ключом. Ключ шифрования для сложения по модулю 2 может быть произвольной последовательностью единиц и нулей. Чтобы зашифровать двоич­ное представление, прибавляют цифры ключа к каждой цифре сообщения. При рас­шифровке вычитают цифры (это то же самое, что и сложение по модулю 2).

Рассмотрим, что получится, если мы будем шифровать сообщение (последователь­ность двоичных цифр), например, 010110, преобразуя ее в другую последовательность, используя ключ «Ключ 1» и «Ключ 0» в некотором произвольном порядке: 110101 (см. рис. 4.22). Согласно правилу, по которому «Ключ 1» заменяет нули сообщения на еди­ницы и наоборот, а «Ключ 0» оставляет все цифры неизменными, получим шифрован­ное сообщение 100011. Это сложение по модулю 2, удобное тем, что вычитание по мо­дулю 2 есть то же самое, что и сложение^ поэтому исходное сообщение может быть восстановлено просто прибавлением последовательности цифр ключа (она известна тому, кому направлено сообщение) к последовательности цифр шифрованного сообщения. Результатом этих преобразований будет расшифрованное сообщение 010110.

Сразу возникает вопрос: имеет ли рассмотренный простой шифр какое-либо практи­ческое значение? Поскольку этот шифр, в сущности, использует лишь две таблицы под­становки минимального размера, очевидно, что мы должны переключаться между ними часто, и делать это случайным образом, то есть прибавлять к данным случайную последо­вательность ключевых цифр. Предположим, это мы сделали. Тогда получим потенциаль­но нераскрываемый шифр. С точки зрения теории информации этот шифр делает следую­щее: к каждому биту информации сообщения прибавляется один бит информации (а точнее, дезинформации!) ключа. Этого достаточно, чтобы полностью разрушить любую структу­ру, которую исходное сообщение могло бы иметь, если только цифры ключа взяты в слу­чайном порядке, скажем, определяемом подбрасыванием монеты, и ключевая последова­тельность имеет такую же длину, как сообщение, и никогда не повторяется.

Стойкость такого метода определяется исключительно тем, что для каждой цифры сообщения мы полностью и случайным образом меняем ключ. Это единственный класс

шифров, для которых можно доказать нераскрываемость в абсолютном смысле этого

слова.

Даже если злоумышленник пытается вскрыть систему с помощью грубой силы, например, опробует все возможные прибавляемые ключи (26 или 64, в случае нашего 6-битного сообщения), он получит все возможные открытые тексты, включая тот, ко­торый мы в действительности зашифровали, но не получит информации о том, какое сообщение правильное. Даже сам дьявол, который мог бы опробовать все возможные ключи в одно мгновение, не мог бы внести определенность. Эта система хорошо изве­стна и используется всеми правительствами под разными именами, такими, как систе­ма Вернама или одноразовый блокнот.

В реальных системах требуется, чтобы на передающей и приемной сторонах были одинаковые ключи, синхронизированные посредством таймера. Цифры сообщения и цифры ключа складываются по модулю 2, полученный в результате зашифрованный поток передается через канал связи, после чего ключ вычитается из данных (прибавля­ется по модулю 2). Для трафика большого объема обширные запасы ключевых цифр должны быть заблаговременно доставлены получателю и храниться у него.

Фундаментальный недостаток системы Вернама состоит в том, что для каждого бита переданной информации получателю необходимо хранить один заранее подго­товленный бит ключевой информации. Более того, эти биты должны следовать в слу­чайной последовательности, и эту последовательность нельзя использовать вторично. Если необходимо шифровать трафик большого объема, то выполнить это требование трудно. Поэтому система Вернама используется только для передачи сообщений наи­высшей секретности.

Чтобы обойти проблему предварительной передачи получателю сообщения сек­ретного ключа большого объема, инженеры и изобретатели придумали много остро­умных схем генерации очень длинных потоков псевдослучайных цифр из нескольких коротких потоков в соответствии с некоторым алгоритмом. Получателя шифрованно­го сообщения при этом необходимо снабдить точно таким же генератором, как и у отправителя. Конечно, такой алгоритм предполагает использование систематических процедур, добавляющих регулярности в шифротекст, обнаружение которых может помочь аналитику дешифровать сообщение.

Один из основных методов построения подобных генераторов заключается в ис­пользовании двух или более битовых потоков, данные которых побитно складываются для получения единого «смешанного» потока. Например, простой длинный поток би­тов ключа может быть заменен двумя циклическими генераторами двоичных последо­вательностей, длины которых являются простыми или взаимно простыми числами (рис. 4.23) Так как в этом случае величины длин двоичных последовательностей не имеют общих множителей, полученный из них поток имеет период повторения, равный про­изведению их длин.

Например, две двоичные последовательности, имеющие длину 1000 и 1001 двоич­ных символов соответственно, дают в результате составной псевдослучайный поток, который не повторяется на первых 10001001, или 1001000 цифрах. Циклические дво­ичные последовательности проходят через сумматор, который складывает по модулю 2 считанные с них цифры. Выход сумматора служит ключом, используемым для за­шифрования сообщения. Поэтому важно, чтобы составной поток превышал по длине

все вместе взятые сообщения, которые могут быть переданы за разумный период вре­мени. Расшифрование осуществляется с помощью ключа, сгенерированного на при­емнике идентичным способом. Таким образом, несколько коротких последовательно­стей заменяют одну длинную, но получающиеся при этом внутренние периодичности могут помочь аналитику в раскрытии шифра.

Поскольку побитовый сумматор является линейным устройством, он изначально криптографически слаб, но может быть усилен разными способами. Можно нагро­мождать одну сложность на другую, вводя цепочки обратной связи* связанные каким-либо образом с передаваемым сообщением, или вводя такие нелинейные математичес­кие операции, как подстановки в блоках цифр подходящего размера. Несекретная криптографическая литература содержит много конструкций генераторов псевдослу­чайных последовательностей, которые могут быть, в принципе, сведены к одной базо­вой схеме, изображенной на рис. 4.24. Тем или иным способом они вырабатывают псевдослучайные числа, выполняя сложные математические операции над упорядо­ченной последовательностью входных чисел, преобразуя их способом, который, как предполагается, должен поставить аналитика в тупик.

В этом обобщенном представлении генератора формирования двоичной ключевой последовательности двоичный счетчик обеспечивает входными числами блок преоб­разований, который вырабатывает биты потока ключа, прибавляемые затем к потоку битов сообщения в зависимости от состояния селектора ключа.

Но даже шифр Вернама на самом деле не обеспечивает защиту от искусного мо­шенничества с трафиком, не обладающим избыточностью.

Независимо от того, закодировано ли сообщение с использованием случайных цифр или псевдослучайной последовательности цифр, в подобном побитовом шифровании одиночная ошибка, возникшая при передаче сообщения, остается в рамках одной циф­ровой позиции; ошибка не «размножается» и не распространяется на остаток сообще­ния. Кроме того, этот шифр не вносит межсимвольных зависимостей. Когда сообще­ние написано на естественном языке, то контекст естественной избыточности позволяет человеку, читающему текст, легко обнаруживать случайные ошибки. Так, если неко-

торые из 5 бит, представляющих букву Е, оказались искаженными таким образом, что соответствующая группа битов стала представлением буквы О (например, слово СЕК­РЕТНЫЙ превратилось в слово СЕКРОТНЫЙ), то читатель-человек, исходя из кон­текста, обнаружил бы ошибку.

Совершенно иная ситуация при использовании компьютеров. Передаваемые дан­ные здесь могут не содержать избыточности, например, если они полностью число­вые, то в этой ситуации ошибка всего в одной цифре может вызвать целый каскад вы­числительных погрешностей. Изучение проблемы показало, что простые коды обнаружения ошибок не подходят для защиты целостности компьютерных данных от возможных подтасовок со стороны злоумышленников. В данном случае необходимо не просто обнаружение ошибок, а требуется аутентификация, защищенная криптогра­фическими методами. Неожиданно оказалось, что это лучше всего достигается, если решение строить на принципах, внутренне присущих шифрующим структурам.

Наибольшая производительность компьютеров достигается при их работе с блока­ми данных длиной 8,16, 32 и т. д. разрядов. Рассмотрим порядок формирования клю­чей для блочных шифров. Блочным шифром будем называть любой шифр, который преобразует п цифр сообщения в п цифр шифрограммы.

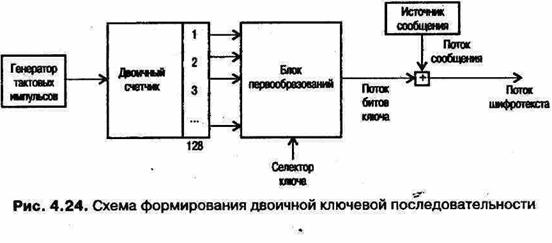
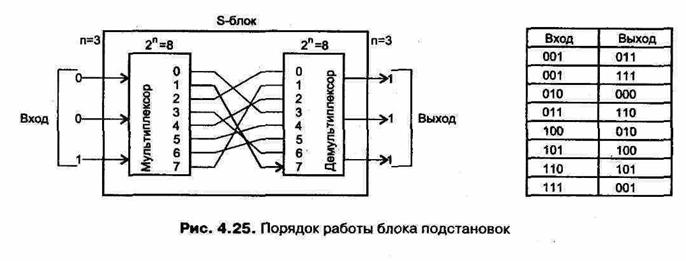
Например, блочным будет такой шифр, который преобразует код 00000, представ­ляющий по нашему соглашению букву А в открытом тексте, в, скажем, 11001, эквива­лент А для шифротекста, по некоторому ключу перестановки, в точности, как это за­дает таблица подстановок. Чтобы увидеть, как такое двоичное преобразование выполняется электронным устройством, давайте рассматривать подстановки только в группах из трех двоичных цифр, как это показано на рис. 4.25.

Блок подстановок, в отличие от потоковых устройств, включает как линейные, так и нелинейные преобразования: он не просто прибавляет нули и единицы к цифрам входа, но может заменить любой входной блок цифр на любой выходной блок. Реаль­но он состоит из двух коммутаторов. Первый преобразует двоичное число из п цифр в одну цифру по основанию 2п, другой выполняет обратное преобразование. Блок, та­ким образом, содержит 2п внутренних соединений коммутаторов, которые могут быть выполнены 2п! различными способами. Это означает, что в случае изображенного на рис. 4.25 блока с п = З^уществует 23! = 8! = 40320 различных вариантов разводки блока или таблиц, подобных той, что изображена на этом рисунке. Блок такого типа с п = 128 сделал бы криптоанализ практически неосуществимым, однако его трудно со­здать технологически.

Рассмотрим, как работает блок подстановок в нашем случае. С помощью трех дво­ичных цифр можно представить восемь элементов: 23 = 8. Устройство, выполняющее подстановку, как мы видим, состоит из двух коммутаторов. Первый (мультиплексор) преобразует последовательность из трех двоичных цифр в соответствующее восьме­ричное значение, подавая сигнал на одну из восьми выходных линий (в нашем случае это линия 1). Эти 8 выходов могут быть соединены с восемью входами второго пере­ключателя любым из 8! (или 40320) способов. Из этого множества различных вариан­тов соединения или коммутации проводов между первым и вторым переключателем мы можем выбрать тот, который будем использовать. Задача второго переключателя (демультиплексора) — преобразовать входной сигнал, представленный одной цифрой по основанию 8, обратно в трехразрядный двоичных выход.

Если бы устройство подстановки было построено для обработки пятицифрового дво­ичного входа, его можно было бы использовать для зашифрования алфавита из 32-х сим­волов. Возможных соединений двух переключателей было бы тогда 32!. Может пока­заться, что ключей очень много, но к созданному таким образом шифру все же необходимо относиться, как к очень слабому: он поддается частотному анализу. Эта слабость не является его неотъемлемым свойством. Рассмотренное устройство с математической точки зрения определяет наиболее общее возможное преобразование. Оно включает для любого заданного размера входа-выхода любой возможный обратимый шифр, который когда-либо был, или даже просто мог бы быть изобретен; математики могли бы сказать, что он представляет полную симметричную группу. Он полностью «несистематичес­кий»: одно соединение переключателей ничего не говорит злоумышленнику относительно всех других соединений. Слабость данного шифра обусловлена выбранным размером блока. Несмотря на большое количество ключей, каталог возможных входов и выходов очень мал: в нем всего лишь 32 элемента. Нам же необходим такой большой каталог, чтобы для любого злоумышленника было практически невозможно записать его. Если взять, например, блок со 128 входами и выходами, то аналитику было бы необходимо рассмотреть 2128 (или больше 1038) возможных блоков цифр. Это настолько огромное число, что частотный анализ здесь просто неосуществим. К несчастью, устройство под­становок со 128 входами также потребовало бы 2128 внутренних соединений между первым и вторым переключателями, что технологически очень сложно реализуется.

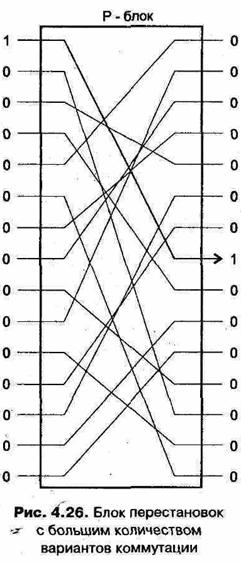
Однако существует преобразование, которое легко реализовать для большого на­бора входов. Практически выполнимо, например, построить блок со 128 входными и выходными выводами, которые внутри соединены обычными проводами, как показано на рис. 4.26.

Для такого «блока перестановок» с п выходами имеется п! возможных вариантов коммутации проводов, каждый из которых определяется отдельным ключом. Он легко может быть построен для п = 128. И хотя это обеспечит большое количество возмож­ных ключей (128!), что весьма полезно, мы теперь столкнемся с новой трудностью. Путем использования набора специально сконструированных сообщений можно це­ликом определить ключ такой системы всего за п-1 попыток (в данном случае 127). Этот прием состоит в том, чтобы использовать серию сообщений, содержащих одну-единственную единицу в п-1 различных позициях. Позиция единицы в выходном бло­ке определит использованное в устройстве подключение провода. Слабость простого блока перестановок заключается в том, что он является линейной системой.

Для повышения стойкости используемого шифра необходим некоторый компро­миссный вариант, который бы, как минимум, приближался по характеристикам к об­щей системе.. Это возможно сделать, используя составной шифр, в котором два или более шифра скомбинированы так, что результирующая система обладает большей стойкостью, чем каждая из составляющих ее систем в отдельности. Перед первой ми­ровой войной были исследованы громоздкие шифры, включающие несколько этапов шифрования. Первым действительно успешным об­разцом была, вероятно, система, изобретенная нем­цами, известная как ADFCVX-система. Она соеди­няла «дробления» с «перестановками». Иными словами, в этой процедуре сообщение разбивалось на сегменты и сегменты переставлялись на другие места. Важный факт, на который следует обратить внимание, заключается в том, что шифр, составлен­ный из блочных шифров, опять является блочным шифром. Цель в том, чтобы шифр вел себя подобно общему шифру замен настолько, насколько это воз­можно.

Между первой и второй мировыми войнами ин­терес к составным шифрам практически полностью пропал благодаря успешному развитию роторных или проводно-дисковых машин, которые принадле­жат к общему классу генераторов псевдослучайных последовательностей. Типичная роторная машина имела клавиатуру, напоминающую клавиатуру пи­шущей машинки. Каждая буква шифровалась с по­мощью нескольких дисков, работающих в опреде­ленной последовательности, для очередной шифруемой буквы диски переводились в другое по­ложение с использованием нерегулярного алгорит­ма, зависящего от ключа. Сообщение расшифровы­валось идентичной машиной с точно таким же установленным ключом.

Сейчас интерес к составным шифрам возник благодаря статье «Теория связи в сек­ретных системах» Клода Шеннона, которая была опубликована в техническом журна­ле корпорации Bell (Bell System Technical Journal) в 1949 году. В разделе, посвящен­ном практической разработке шифров, Шеннон ввел в рассмотрение понятия «перемешивания» и «рассеивания», а также понятие «перемешивающего преобразо­вания», которое предполагает особый способ использования результатов преобразо­вания. Его статья открыла практически неограниченные возможности по разработке и исследованию шифров.

Способ, которым следует сочетать принципы перемешивания и рассеивания для получения криптографической стойкости, можно описать следующим образом: пере­становки общего вида не могут быть реализованы для больших значений п, скажем, для п = 128, и поэтому мы должны ограничиться схемами подстановки, имеющими практический размер. Например, в системе «Люцифер» для блоков подстановки выб­рано п = 4. Хотя это число может показаться слишком маленьким, такая подстановка может оказаться вполне эффективной, если ключ подстановки или схема коммутации проводников выбраны верно. В системе «Люцифер» нелинейная подстановка эффек­тивно обеспечивает определенную степень перемешивания.

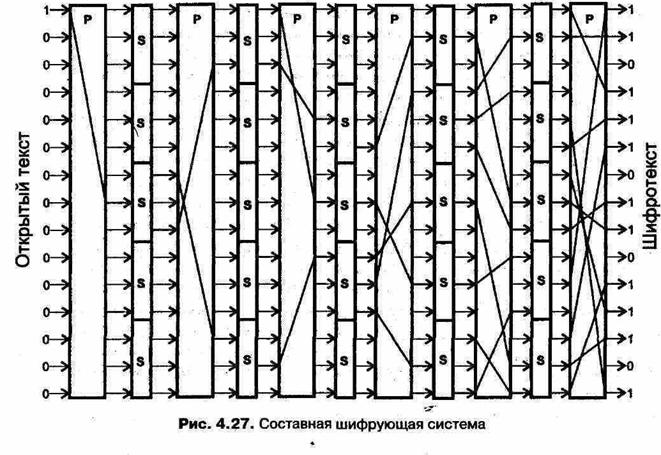
В этой системе входные данные пропускаются через чередующиеся уровни блоков, которые обозначены на предыдущих рисунках символами Р и S. В блоке перестановок Р п — большое число (128 или 64), а в блоке подстановок S число п мало (4). Несмот­ря на то, что Р- и S-блоки в отдельности составили бы слабую систему, в комбинации друг с другом они устойчивы.

Проиллюстрируем меру стойкости подобных конструкций на примере устройства (составной шифрующей системы), изображенного на рис. 4.27, в котором для просто­ты Р-блоки имеют размер п = 15, а S-блоки — п — 3. Если изобразить этот «бутерброд» из блоков со специально сконструированным входным числом, составленным из 14 нулей и одной-единственной единицы, то легко будет увидеть перемешивание и рассе­ивание в работе. Первый блок Р передает единственную единицу на вход некоторого блока S, который, будучи нелинейным устройством, может преобразовать единицу в трехцифровой выход, содержащий в потенциале целых 3 единицы. В показанном на диаграмме варианте он вырабатывает две единицы. Следующий блок Р тасует две еди­ницы и передает их на вход двух различных S-блоков, которые вместе имеют потенци­ал по выработке уже шести единиц. Дальше диаграмма говорит сама за себя: по мере того, как входной блок данных проходит через последовательные уровни, узор из сге­нерированных единиц расширяется и дает в результате непредсказуемый каскад цифр. Конечный результат, получающийся на выходе всей цепочки, будет содержать в сред­нем половину нулей и половину единиц, в зависимости от ключей перестановки, ис­пользованных в различных Р-и S-блоках.

Очень важно, что все выходные цифры потенциально стали сложными функциями всех входных цифр. Поскольку все блоки имеют независимые ключи, поток вырабаты­ваемых цифр и окончательный результат не могут быть предсказаны. Цель разработ­чика, конечно, — сделать предельно трудным для злоумышленников прослеживание цепочки назад и, таким образом, реконструировать ключи в Р- и S-блоках.

В реальной системе S-блок, например, являясь достаточно общим преобразовани­ем, может случайно быть снабжен таким ключом, что поведет себя в точности как Р-блок, и в этом случае вся система будет не более стойкой, чем один слой Р, который может быть достаточно просто раскрыт. Чтобы этого избежать, блоки обоих типов снабжают постоянными ключами, которые должны быть сильными; эти постоянные ключи будут известны каждому, кто имеет доступ к системе. Следовательно, необхо­дим другой способ использования ключей, при этом желательно, чтобы они могли быть представлены двоичными числами. Этого можно достигнуть, построив «бутерброд», в котором каждый S-блок содержит два различных постоянных ключа, и, таким обра­зом, может быть представлен двумя возможными различными состояниями — SO и S1. Последовательность этих состояний для любого отдельного «бутерброда» состав­ляет управляемую ключом структуру, не известную потенциальному противнику. Эту структуру можно представить двоичным ключом, который указывает, которую из двух таблиц подстановки следует использовать, в точности как в случае двухтабличной подстановки, рассмотренной выше. Цифры ключа можно загрузить в ключевой ре­гистр криптографического устройства и записать на ключевую магнитную карту, зак­репленную за законным пользователем системы. Когда два состояния S-блоков ис­пользуются подобным образом, результирующая криптограмма показывает межсимвольные зависимости, которые делают все цифры выхода сложными функция­ми не только всех цифр входа, но и всех цифр ключа. Таким образом, эта система устойчива к попыткам проникновения в нее с помощью математических методов ана­лиза.

Хотя межсимвольная зависимость — необходимый (но не достаточный) показа­тель криптографической стойкости, она имеет и оборотную сторону: влечет за собой чувствительность системы к шуму или помехам во время передачи. Погрешность в

единственной цифре может привести к полному искажению расшифрованных данных. Современные средства коммуникации делают, однако, эту проблему менее актуаль­ной, по крайней мере, для невоенного использования.

Более того, сильные взаимозависимости между цифрами могут принести удиви­тельную и неожиданную пользу: поскольку система так чувствительна к изменениям и так резко реагирует на них, она автоматически становится идеальным средством обнаружения изменений, произошедших как случайно, так и сделанных умышленно. В результате получаем одновременно высокую секретность сообщений и неподдаю­щийся обману сигнализатор ошибок.

Чтобы извлечь пользу из этой дополнительной особенности шифра, необходимо все­го лишь зарезервировать место для пароля внутри заданного блока цифр сообщения. Пароль — это последовательность цифр, автоматически вводимая в поток цифр сообще­ния передающей аппаратурой без какого-либо участия лица, использующего систему. Роль пароля заключается в том, чтобы сообщить приемной аппаратуре, что сообщение не было преднамеренно искажено или серьезно испорчено шумом в процессе передачи. Процесс зашифрования оставляет противника в неведении, как биты сообщения и паро­ля отображены в криптограмме. Если цифры пароля не могут быть без ошибок восста­новлены декодером на принимающем конце, сообщение отвергается.

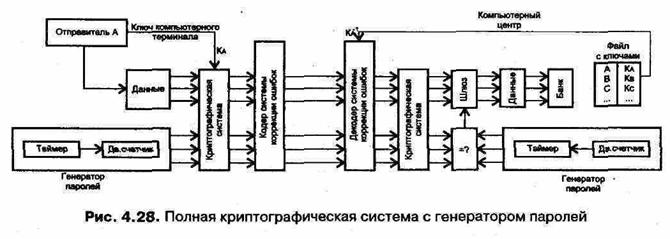
Решающую роль в этой схеме играет генератор пароля, который должен быть как на приемнике, так и на передатчике, как показано на рис. 4.28. Генератор пароля на самом деле является не чем иным, как двоичным таймером или счетчиком, определяю­щим время или порядковый номер сообщения в двоичной записи, и добавляющим эту группу цифр к каждому блоку цифр передаваемого сообщения. Необходимо учесть, что в определенный момент времени, скажем в 8:00, таймеры на обоих концах канала передачи должны быть синхронизированы и иметь одинаковые частоты.

Полная система объединяет генератор пароля, криптографическую систему, со­стоящую из S- и Р-блоков и систему коррекции ошибок. Генератор паролей вырабаты­вает новый парольный блок для каждого блока данных. Отправитель, используя пер­сональный ключ, вводит свои данные. Цифры пароля и данных станут не отслеживаемыми после того, как будут зашифрованы в соответствии с ключом. До­полнительные цифры кода коррекции ошибок добавляются к данным перед передачей и изымаются сразу после приема. Криптографическая система компьютерного центра расшифровывает передачу в соответствии с инвертированным ключом отправителя,

который выбирается из специального защищенного файла, хранимого в центре, и из­влекает цифры пароля. Если они совпадут с цифрами пароля, сгенерированного в ком­пьютере, шлюз открывается и входные данные передаются в хранилище.

А как же «парольная схема аутентификации» обеспечивает безопасность работы членам сообщества пользователей централизованного хранилища данных, которые имеют доступ к большому центральному компьютеру? Рассмотрим и этот вариант. Каждый пользователь имеет свой собственный секретный ключ, возможно, представ­ленный в форме последовательности двоичных цифр, записанной, например, на маг­нитную карту или смарт-карту. Ключи всех пользователей хранятся в защищенной форме в центральном компьютере. Предположим, что пользователь с ключом КА хо­чет передать сообщение на центральный компьютер. Он вставляет карточку, на кото­рой записан его ключ, в считывающий терминал, располагающийся на его рабочем столе, секунду или две ждет сигнала, что линия свободна, и начинает набирать свое сообщение.

Сообщение автоматически разделяется на блоки цифр (скажем, по 64 цифры), кото­рые на каждом сигнале двоичного таймера объединяются с паролем (который также может иметь 64 цифры), соответствующим выходу таймера в этот момент времени. Результи­рующий блок из 128 цифр шифруется, для чего пропускается через криптосистему Р- и S- блоков, которая полностью перемешивает цифры пароля и цифры данных.

Поскольку результирующая криптограмма очень чувствительна к ошибкам пере­дачи, она усиливается с помощью кода исправления ошибок, который реагирует на шум в используемых линиях связи. Добавление этого кода удлиняет блок, содержа­щий цифры пароля и сообщения, еще на несколько цифр.

Результирующий блок шифрограммы дополняется адресом отправителя в откры­том виде и передается на центральный компьютер. Когда сообщение доходит до адре­сата, ключ КА, принадлежащий пользователю А, отыскивается в соответствующем списке и его обращение загружается в декодер для того, чтобы расшифровать крипто­грамму.

Будет ли совпадать пароль из полученной криптограммы с паролем, локально вы­работанным двоичным таймером на принимающей стороне? При отсутствии искаже­ний, и если криптограмма была действительно зашифрована на ключе пользователя А, выход декодера будет состоять из блока цифр данных и блока цифр правильного пароля. Это считается достаточным свидетельством в пользу того, что криптограмма действительно создана пользователем А и система принимает данные.

Что же случится, если произошло искажение данных? Если оно было вызвано шу­мовыми всплесками в линии связи, то код исправления ошибок устранит его и сообще­ние успешно пройдет аутентификацию. Если же искажения не могут быть устранены кодом коррекции ошибок, то даже одна неверно принятая цифра произведет эффект лавины в декодирующем устройстве и превратит всю принятую информацию в мусор. Пароли больше не будут совпадать. Система воспримет сообщение, как имеющее по­дозрительное происхождение, и отвергнет его.

Решающим шагом является проверка того, что парольный тест сработал бы так же надежно, если кто-либо записал бы перехваченное сообщение и повторно передал его позже, когда пароль перестал быть действительным. Конечно, использование невер­ного ключа — причина для немедленной отбраковки сообщения. Представляется, что предложенная система устойчива к любой мыслимой попытке обмануть ее. Каждая двоичная цифра пароля обеспечивает один бит аутентифицирующей информации. Если пароль состоит из п цифр, то злоумышленник имеет лишь один шанс из 2п (или один шанс из 264, если п = 64) сгенерировать любым способом такую криптограмму, кото­рая при расшифровке случайно даст истинный пароль. Число 264 равно примерно 1019. Невозможно аутентифицировать данные более эффективно.

Дата добавления: 2014-01-07