Термодинамическое обоснование законов Коновалова

Для идеальных жидких растворов из двух компонентов (А и В), па которых также можно считать идеальным газом, согласно закону Рауля можно записать

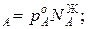pp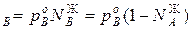

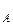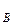где р,р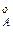,р,р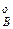– парциальное давление компонентов А и В раствора и чистых веществ соответственно; N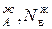– мольные доли компонентов А и В соответственно в жидком растворе.

Поделим эти два уравнения друг на друга и получим:

(1)

Из уравнения состояния можно определить мольную долю компонента А в паровой фазе:

р_АV=N_А^пRT

p_BV=N_B^пRT=(1-N_A^п)RT, т.е.

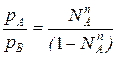(2)

где N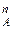– мольная доля компонента А в паровой фазе.

Приравнивая уравнения 1 и 2,получим

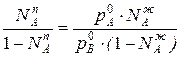
Отношения между мольными долями компонентов в паровой и жидкой фазах можно выразить следующим образом:

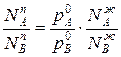(3)

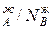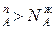Уравнение 3 показывает изменение состава жидкости и пара в соответствии с законами Коновалова. Действительно если р_A⁰> р_В⁰ (см.диагр.2), то N_A^п / N_В^п >N, Nи подтверждается условие N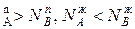,характеризующее первый закон Коновалова. Если р_A⁰= р_В⁰, то правая и левая части уравнения

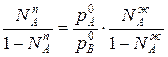
равны и становится справедливым равенство N_A^п = N_A^ж; N_Вⁿ= N_В^ж. Условие равенства парциальных давлений компонентов А и В соответствует азеотропной точке О, что фиксируется вторым законом Коновалова.

Анализ уравнения (*).

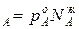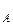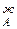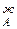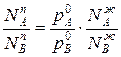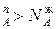С ростом концентрации компонента А его парциальное давление, согласно условию р, всегда растет и увеличивается на dp/dN. Одновременно растет общее давление р за счет более летучего компонента А. При dp/dN>0 согласно уравнению , N, и подтверждается условие 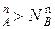N, N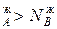,а пар обогащается более летучим компонентом, что соответствует первому закону Коновалова.

Для определения экстремума на кривой, описываемой уравнением 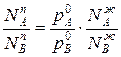необходимо предположить, что dp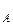/dN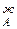=0. Это означает 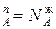N, N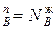, характерное для азеотропных точек в соответствии со вторым законом Коновалова.

Дата добавления: 2014-01-07