Вопросы для самлконтроля

S1 S1

C1 C1

О1 O1

S2 A1 31 S2 A1

B1 B1

B2 B2

·

D1 D1

Рис. 8,б Восстановление Рис. 8,в Определение

перпендикуляра и нахождение видимости граней пирамиды

натуральной величины

5. Определим натуральную величину высоты пирамиды методом вращения горизонтальной проекции перпендикуляра ОS1 (рис. 8,б).

6. Отрезок (O1S¢) является натуральной величиной ^ [SО] = 50 мм. (рис. 8,в).

7. Достроим недостающие ребра и грани пирамиды и определим видимость ребер с помощью конкурирующих точек (рис. 8,в).

Пример 4. Найти натуральную величину плоскости ∆ АВС и угол его наклона к плоскости проекций П₁ (рис. 9).

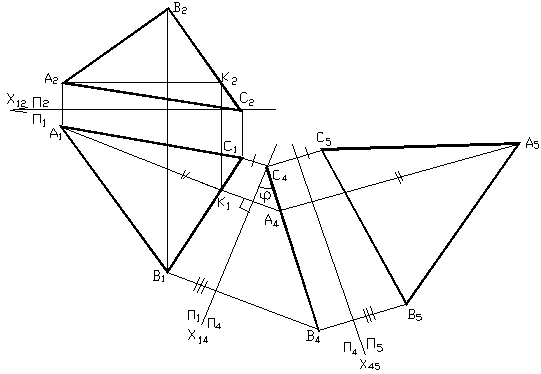
Рис. 9 Нахождение натуральной величины плоскости методом замены плоскостей проекций

Выберем новую плоскость проекций П₄, перпендикулярную плоскости треугольника АВС, а на чертеже – перпендикулярную горизонтали АК плоскости треугольника - П₄ ^ ∆ АВС, П₄ ^ АК, АК Î ∆АВС, АК || П₁.Проводим новую ось координат X₁₄ ^ А₁К₁. Имеем систему взаимно перпендикулярных плоскостей П₁ ^ П₄. Плоскость ∆ АВС по отношению к плоскости П₄ будет проецирующей. Проводим линии проекционной связи от точек А₁, В₁ и С₁ и откладываем координаты Z вершин треугольника от новой оси X₁₄, получаем проекции точек А_4, В₄, С₄. Проекции ∆ АВС на П₄ – прямая С₄ В₄, составляющая с осью X₁₄ угол, равный натуральной величине угла между плоскостью треугольника и плоскостью П₁ – угол φ.

Чтобы найти натуральную величину треугольника вместо плоскости П₁ вводим новую плоскость П₅ плоскости треугольника. Параллельно проекции треугольника С₄ В₄ проводим новую ось X₄₅. На линиях проекционной связи отложим от новой оси отрезки, равные расстояниям от заменяемых проекций вершин А₁, В₁, С₁ до заменяемой оси X₁₄. А₅В₅С₅ – натуральная величина треугольника. А₅В₅С₅ = |АВС|

В проектной деятельности часто встречаются задачи на преобразование комплексного чертежа. Эти задачи, в основном, связаны с нахождением натуральных величин углов, прямых, плоскостей сечений любых геометрических фигур. Можно применять и метод плоскопараллельного перемещения для нахождения натуральных величин объектов.

2. Метод плоскопараллельного перемещения в пространстве – это такое перемещение, при котором все точки геометрической фигуры перемещаются в плоскостях, параллельных какой либо плоскости проекций без изменения вида и размеров этой фигуры.

Если все точки геометрической фигуры двигаются в плоскостях, параллельных плоскости проекций П₁, то горизонтальная проекция этой фигуры перемещается, не меняя формы и размеров, а вертикальные проекции всех точек фигуры перемещаются по прямым, параллельным оси X.

Если все точки геометрической фигуры двигаются в плоскостях, параллельных П_2, то фронтальная проекция этой фигуры перемещается, не меняя формы и размеров, а горизонтальные проекции всех точек фигуры перемещаются по прямым, параллельным оси X. Можно провести и двукратное перемещение геометрической фигуры. При перемещении сохраняется угол наклона геометрической фигуры (прямых, плоскостей) к данной плоскости проекций.

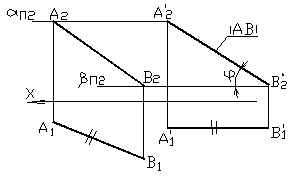
Пример 5. Прямую общего положения АВ преобразовать во фронталь и определить ее натуральную величину и угол наклона к горизонтальной плоскости проекций П₁ (рис. 10).

Перемещением переводим отрезок прямой АВ в положение, параллельное П₂. Для этого в произвольном месте чертежа горизонтальную проекцию А₁В₁ отрезка АВ располагаем горизонтально, параллельно

– А₁'В₁' || OX, А₁'В₁' = А₁В₁ Точки А и В отрезка перемещаются соответственно в горизонтальных плоскостях a и b - АÎa Ù a || П₁, ВÎb Ùb || П₁.

Фронтальные проекции А₂ и В₂ точек А и В перемещаются по a_П2 и b_П2. Фронтальные проекции А₂' иВ₂' смещенных точек А' и В' находятся в проекционной связи с проекциями А₁' и В₁'. А₂'В₂' – новая фронтальная проекция отрезка АВ – А₂'В₂' = |АВ|.

Угол наклона А₂'В₂' к оси координат OX является натуральной величиной угла наклона отрезка АВ к плоскости проекций П₁. А₂'В₂' ÙOX = АВ Ù П₁.

Пример 6. Определить натуральную величину ∆АВС и угол его наклона к плоскости проекций П₁ (рис. 11).

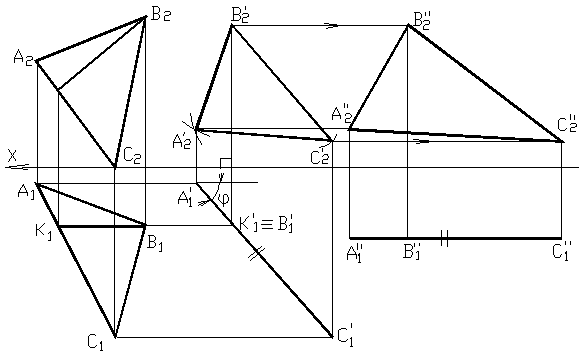
Рис. 6 Плоскопараллельное перемещение плоскости для нахождения натуральной величины треугольника АВС

Задача решается двумя последовательными перемещениями. Первым перемещением ∆АВС приводится в положение, перпендикулярное горизонтальной плоскости проекций П₁. Вторым перемещением он приводится в положение, параллельное фронтальной плоскости проекций П₂.

Для этого в плоскости ∆АВС проводим фронталь ВК. Перемещаем фронталь ВК в положение горизонтально проецирующей прямой – ВК ^ П₁. При этом плоскость треугольника станет горизонтально проецирующей плоскостью. На чертеже проводим следующие построения. Фронтальную проекцию В₂К₂ располагаем перпендикулярно оси координат OX. Величина фронтальной проекции треугольника при этом не меняется. Строим фронтальную проекцию треугольника А₂'В₂'С₂',учитывая равенство сторон –

А₂В₂ = А₂'В₂', А₂С₂ = А₂'С₂', В₂С₂ = В₂'С₂'.

Горизонтальной проекцией А₁В₁С₁ треугольника в новом положении является отрезок прямой А₁'С₁', угол наклона которого к оси OX является натуральной величиной угла наклона плоскости треугольника к плоскости П₂ – угол ψ.

Чтобы получить натуральную величину треугольника, переместим новую горизонтальную проекцию треугольника (прямую А₁'С₁') на свободное место чертежа в положение, параллельное оси OX. Плоскость треугольника станет плоскостью уровня. Фронтальные проекции точек при этом перемещаются параллельно оси ОX (сохраняется неизменной координата Z точек). На фронтальной проекции имеем натуральную величину плоскости ∆АВС - А₂''В₂''С₂'' = |∆АВС|.

Существует еще один метод нахождения натуральных величин объектов это метод вращения. Он описан в литературе достаточно подробно, и вы изучите его самостоятельно.

1. В чем заключается общий прием построения линии пересечения двух плоскостей?

2. Как определяется видимость двух фигур на плоскостях проекций?

3. Сформулируйте теорему о перпендикуляре к плоскости.

4. Как определить расстояние от точки до плоскости?

5. Какова цель способов преобразования чертежа?

6. В чем сущность преобразования проекций способом замены плоскостей проекций?

7. Какое перемещение геометрических объектов в пространстве называют плоскопараллельным?

8. Как располагается плоская фигура при использовании способа вращения ее вокруг оси, параллельной плоскости проекций?

Дата добавления: 2014-01-07