Методы определения деформаций

Деформации оснований

В общем случае осадка фундамента может складываться из следующих составляющих:

S = S ₁ + S ₂ + S ₃ + S ₄. (5.3)

При разработке котлована происходит разгрузка грунта и упругое поднятие дна после загрузки основания весом, равным весу вынутого грунта, в результате чего фундамент получит дополнительную осадку, называемую осадкой разуплотнения S ₁.

Осадки уплотнения S ₂ возникают вследствие уменьшения объема пор от давлений, передаваемых на основание через подошву фундамента. При этом давления должны быть больше структурной прочности. Если осадки уплотнения окажутся различными для фундаментов в пределах одного и того же здания, то они будут неравномерными. Нужно так запроектировать фундаменты, чтобы разность осадок была меньше предельно допустимой.

СНиП допускают развитие в краевых участках фундамента зон пластической деформации на глубину 1/4 ширины фундамента. Образование этих зон и приводит к возникновению осадок неупругого деформирования S ₃.

При разработке котлованов тяжелыми механизмами, при промерзании и оттаивании грунтов, их набухании, замачивании и других явлениях происходит нарушение естественной структуры и увеличивается сжимаемость грунтов, что и является причиной возникновения осадки расструктуривания S ₄.

Расчет деформации оснований осуществляется с использованием расчетных моделей:

- линейно-деформируемого слоя ограниченной мощности;

- линейно-деформируемого полупространства;

- местных упругих деформаций;

- нелинейно-деформируемой среды.

1. Расчетная схема в виде линейно-деформируемого слоя принимается при следующих условиях:

а) в пределах сжимаемой толщи Н _сж, определенной для линейно-деформируемого полупространства, залегает слой грунта с модулем деформации Е ₁ > 100 МПа и толщиной h ₁. При этом

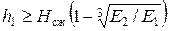, (5.4)

где Е ₂ – модуль деформации грунта, подстилающего слой грунта с модулем деформации Е ₁;

б) ширина фундамента b ³ 10 м и модуль деформации грунтов основания E ³ 10 МПа.

2. Расчетная схема в виде линейно-деформируемого полупространства применяется для расчета осадок фундаментов на однородном основании.

При использовании этой схемы напряжения и деформации в основании определяются с использованием решений теории линейно-деформируемой среды. Для круглых и квадратных фундаментов используется решение Буссинеска, а для ленточных фундаментов - решение Фламана. В схеме линейно-деформируемого полупространства вводится ограничение в виде сжимаемой толщи основания Н _сж. Из условия отношения дополнительных вертикальных напряжений от внешней нагрузки s _z к собственному весу грунта

s_пр = g z. (5.5)

Для определения Н _сж принимается, что s _z = 0,2s_пр.

3. Модель местных упругих деформаций учитывает лишь упругие деформации непосредственно в месте приложения нагрузки.

4. Применение теории нелинейно-деформируемой среды позволяет рассчитывать осадку фундамента вплоть до предельной нагрузки по устойчивости.

5.3.1. Метод общих упругих деформаций

Этот метод базируется на строгом решении теории упругости для упругого полупространства и для упругого слоя ограниченной конечной толщины, лежащей на несжимаемом основании. Решение будет справедливо и для определения общих деформаций (упругих и остаточных) линейно-деформируемого полупространства и линейно-деформируемого слоя грунта ограниченной толщины.

Исходной зависимостью при определении общих упругих деформаций полупространства является формула Ж.Буссинеска

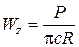, (5.6)

где c – коэффициент упругого полупространства,

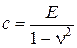. (5.7)

Если рассматривается линейно-деформируемое полупространство, то модуль упругости грунта Е следует заменить на модуль общей деформации (упругой и остаточной) Е ₀, а коэффициент Пуассона n – на коэффициент общей относительной деформации n₀.

При действии на упругое полупространство местной равномерно распределенной нагрузки P по площадке F осадка любой точки определяется путем интегрирования выражения для вертикальных перемещений точки упругого полупространства от действия элементарной сосредоточенной силы Pd x d h (рис.5.3):

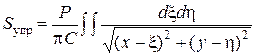. (5.8)

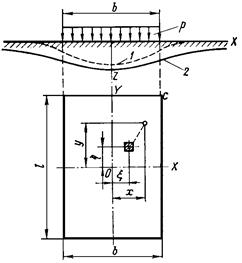
Рис.5.3. Схема действия местной нагрузки: 1 – деформация упругого слоя ограниченной толщины; 2 – деформация упругого полупространства

Решение получено для определения осадок круглых, квадратных и прямоугольных фундаментов.

В общем случае формула (5.8) приведена к виду

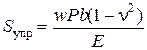, (5.9)

где w – коэффициент формы площади подошвы и жесткости фундамента; b – ширина фундамента; P – удельное давление на грунт; E и n – модули упругости полупространства.

Придав обозначениям для модулей общей деформируемости индекс 0, получим

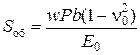, (5.10)

значения w табулированы для определения: w_с – для осадки угловых точек прямоугольной площади загрузки; w ₀ – для максимальной осадки под центром загруженной площади; w_m – для средней осадки загруженной площади; w _const – для осадки абсолютно жестких фундаментов; w_mh – для средней осадки прямоугольных площадей загрузки на слое грунта ограниченной толщины при b/h = 0,25, 0,5, 1, 2, 5 (табл.IV.1 приложения IV).

5.3.2. Метод местных упругих деформаций

Этот метод учитывает лишь упругие деформации непосредственно в месте приложения нагрузки и базируется на гипотезе Фусса - Винклера, согласно которой давление в данной точке прямо пропорционально лишь местной осадке грунта в этой точке:

P = c_zz, (5.11)

где P – давление, Па; c_z – коэффициент упругости основания, называемый коэффициентом постели, Н/см³, z – вертикальное упругое перемещение, м,

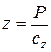. (5.12)

Осадка будет происходить лишь в месте приложения нагрузки, где Р =0, очевидно, z = 0 (см. рис.3.6).

Отметим, что на гипотезе (5.11) базируется вывод основного дифференциального уравнения изгиба фундаментных балок и плит, опирающихся на сплошное (винклеровское) упругое основание. Из курса сопротивления материалов и теории упругости известно, что это дифференциальное уравнение имеет вид

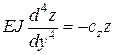, (5.13)

где EJ – жесткость фундаментной балки; z – упругий изгиб балки.

Дата добавления: 2014-01-07