Плоская и пространственная задачи теории фильтрационной консолидации

Дифференциальные уравнения консолидации. Для плоской и пространственной задач дифференциальные уравнения теории фильтрационной консолидации сформулированы проф. В.А.Флориным, и их можно записать в следующем виде:

для плоской задачи

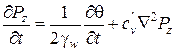, (5.74)

где 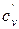– коэффициент консолидации для плоской задачи, 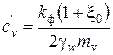(здесь x₀ – коэффициент бокового давления грунта в состоянии покоя); q –сумма главных напряжений в рассматриваемой точке от действия внешней нагрузки; 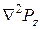– оператор Лапласа для плоской задачи, ;

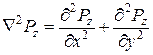для пространственной задачи

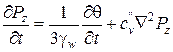, (5.75)

где 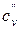– коэффициент консолидации для пространственной задачи, ; 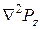– полный оператор Лапласа, .

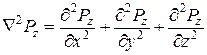Если в результате решения соответствующего дифференциального уравнения консолидации будет найдено эффективное напряжение для данного времени t, то осадка S_t определится по формуле

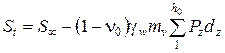, (5.76)

где 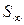– полная стабилизированная осадка; h ₀ - мощность сжимаемой толщи.

Действие равномерно распределенной нагрузки по прямоугольной площадке. Г.Гиббсоном и Г.Мак-Нейми получено следующее выражение для степени уплотнения U_c угловой точки прямоугольной площади загрузки:

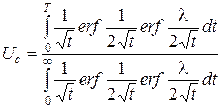, (5.77)

где T – фактор времени, , (здесь 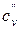– коэффициент консолидации; L – длина прямоугольной площади загрузки); l – отношение сторон прямоугольной площади.

Для практических расчетов построены кривые, позволяющие по величине 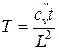определить для ряда значений l (рис.5.17) степень консолидации U_c.

Рис.5.17. Кривые Гиббсона для определения степени консолидации грунта под угловой точкой с прямоугольной площади загрузки

Полная осадка угловой точки S_c определяется по формуле

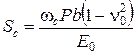, (5.78)

где w _с – коэффициент формы для угловой точки с; Р – удельная нагрузка по прямоугольной площади загрузки; b – ширина загруженной площади.

Зная осадки S_c и степень консолидации U_c, определяем осадку угловой точки во времени t:

S_t = S_cU_c. (5.79)

Пользуясь методом угловых точек и приведенными на рис.5.17 кривыми, можно определить осадку в любой точке массива грунта.

Дата добавления: 2014-01-07