Зависимость между внешним давлением и изменением коэффициента пористости

Уплотнение грунта под действием внешнего давления можно рассматривать по трем основным схемам:

1) сжатие без ограничения возможности бокового расширения, так называемое одноосное сжатие (рис.2.1,а), характерное для передачи нагрузки на свободный образец грунта (по типу испытания на сжатие твердых тел);

2) сжатие грунта нагрузкой, передаваемой на часть поверхности грунта, при ограниченной возможности бокового расширения (рис.2.1,б), так называемое трехосное сжатие (по типу давления на грунт от фундаментов);

3) сжатие грунта нагрузкой, равномерно распределенной по безграничной поверхности грунта, без возможности бокового расширения (рис.2.1, в), так называемое компрессионное сжатие (по типу передачи равномерно распределенной нагрузки от фундамента больших размеров на слой грунта ограниченной мощности, подстилаемый жестким основанием).

Компрессионная зависимость предусматривает работу грунта по схеме рис.2.1в, т.е. сжатие без возможности бокового расширения.

Рис.2.1. Схемы уплотнения грунта

При уплотнении грунта под нагрузкой происходит выдавливание воды из пор, а если, кроме того, поры заполнены воздухом, то выдавливается и воздух.

Особенность протекания процесса деформации грунта представляет ее зависимость от времени. Время деформации может исчисляться годами, десятилетиями, а иногда – столетиями: оно зависит от скорости отжатия воды и воздуха, т.е. от размера пор, рода воды, взаиморасположения пор, сопротивления трению и сцеплению между частицами грунта. Так, пленочная вода перемещается очень медленно, наличие защемленного воздуха в закрытых порах может значительно осложнить деформации. В большинстве случаев деформация уплотнения грунта определяет в целом деформацию сооружения, поэтому изучение законов уплотнения грунта представляет собой важнейшую задачу.

Сжатие без возможности бокового расширения ведут на так называемых компрессионных приборах (одометрах), моделирующих работу грунта. Для исследований используют образцы грунта ненарушенной структуры, отобранные в жесткие металлические кольца.

Рис.2.2. Схема компрессионного прибора (одометр):

1 – индикаторы, 2 – жесткое кольцо, 3 – пористые штампы

Нагрузку на грунт передают ступенями, выдерживая каждую ступень до полного затухания деформаций. Замер деформаций производят мессдозами. По изменению высоты образца грунта определяют изменение коэффициента пористости.

Зависимость между величинами давления P и величинами коэффициента пористости e грунта наносят на график. Соединяя опытные точки, получают компрессионную кривую (рис.2.3).

Для полностью водонасыщенных грунтов по оси ординат вместо коэффициента пористости можно откладывать весовую влажность. Компрессионную кривую можно строить и в координатах

,

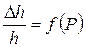где 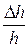– относительное сжатие образца грунта высотой h.

Рис.2.3. Компрессионная кривая

Очертание компрессионной кривой свидетельствует о том, что при первоначальном обжатии грунта происходит его значительное уплотнение, а по мере увеличения давления уплотняемость грунта уменьшается. Очевидно, что в начале обжатия из грунта сравнительно легко выдавливается свободная вода, затем наступает сжатие воды рыхло-связанной, и, наконец, остается прочно-связанная вода, которую практически сжать не удается; кроме того, сжимаемость грунта уменьшается в связи с увеличением прочности и нарастанием числа контактов между частицами.

К проведению компрессионных испытаний предъявляют следующие требования:

1) для уменьшения искажения результатов за счет трения грунта о стенки кольца необходимо применять образцы с отношением диаметра к высоте ;

2) для воссоздания природных условий работы грунта под сооружением следует перед началом испытания обжать образец тем давлением от собственного веса грунта, которым он был обжат в природных условиях, т.е. так называемым “бытовым давлением” (величина обжатия зависит от глубины, с которой был взят образец);

3) при испытании полностью водонасыщенных грунтов, содержащих в порах свободную воду (так называемая “грунтовая масса”), нужно перед началом испытания подвести к образцу воду для снятия с поверхности образца капиллярного давления менисков, могущего исказить действительную картину работы грунта под нагрузкой (часть внешнего давления может оказаться израсходованной на снятие давления менисков).

Если после уплотнения образца внешним давлением произвести его разгрузку, то деформации восстановятся тем полнее, чем выше упругие свойства грунта (рис.2.4).

Рис.2.4. График загрузки и разгрузки образца грунта: 1 – ветвь нагрузки (уплотнения); 2 – ветвь разгрузки (набухания)

При подведении к образцу воды, последняя будет втягиваться в поры грунта, вызывая его набухание.

При испытании “грунтовой массы” экспериментальная компрессионная кривая имеет правильную логарифмическую форму. Если во время испытания производить многократное разгружение с последующим загружением большей по величине нагрузкой, то кривая приобретает петли гистерезиса, а опытные точки, характеризующие зависимость коэффициента пористости от давления, разместятся на той же компрессионной кривой логарифмической формы, называемой главной ветвью уплотнения (рис.2.5).

Рис.2.5. Главная ветвь компрессионной кривой (при циклической разгрузке и нагрузке образца грунта)

Очевидно, если когда-то в прошедшие времена грунт в природных условиях был обжат внешним давлением, а впоследствии это давление было устранено, то это обязательно отразится на очертании компрессионной кривой.

Степень сжимаемости грунтов, не обладающих структурной вязкостью, зависит от первоначальной пористости. Грунты с жестким скелетом (пески), обычно менее сжимаемы, чем грунты с упругим скелетом (глина). Грунты нарушенной структуры сжимаемы значительно больше, чем грунты ненарушенной структуры при одной и той же начальной пористости (рис.2.6).

Рис.2.6. Компрессионные кривые грунта ненарушенной структуры (1) и перемятого грунта (2)

Для грунтов естественной ненарушенной структуры компрессионная кривая имеет два участка (рис.2.7): первый – до давлений, не превосходящих структурную прочность грунта P _стр с очень малыми изменениями коэффициента пористости, и второй – со значительными изменениями коэффициента пористости, что указывает на уплотнение грунта под нагрузкой, превосходящей структурную прочность грунта. Структурная прочность является важной характеристикой грунта, и ее значение можно определить по компрессионной кривой ненарушенной структуры грунта при малых ступенях нагружения (0,002…0,010 МПа). Резкий перелом компрессионной кривой и будет соответствовать достижению структурной прочности сжатия.

Рис.2.7. Компрессионные кривые для грунта ненарушенной структуры

Более общим методом построения компрессионных кривых является метод определения коэффициента пористости по осадкам образцов грунта при уплотнении их в компрессионном приборе. Обозначим е ₀ начальный коэффициент пористости грунта, определяемый по формуле

, (2.1)

где n – объем пор грунта, m_s – объем скелета.

Очевидно, что n + m = 1, тогда

, , .

Коэффициент пористости грунта при любой ступени нагрузки

,

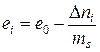где D n_i – изменение пористости грунта от начала загружения; m – объем твердых частиц во всем объеме грунта.

При испытании образца грунта без возможности бокового расширения грунта изменение объема пор D n_i численно равно произведению осадки S_i и площади образца F:

.

Объем твердых частиц во всем объеме грунта равен

,

здесь h – начальная высота грунта.

После соответствующих подстановок получим

. (2.2)

Этой формулой пользуются для вычисления коэффициентов пористости, соответствующих данным ступеням нагрузки, а по ним строят и всю компрессионную кривую.

Математическое выражение закона уплотнения может быть найдено из анализа участка компрессионной кривой, заключенного между бесконечно близкими точками А и В (рис.2.8). При приращении внешнего давления D P произойдет уменьшение коэффициента пористости D e.

Можно записать

.

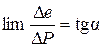Тангенс угла наклона отрезка компрессионной кривой к оси давлений tg a характеризует сжимаемость грунта в рассматриваемом диапазоне давлений и носит название коэффициента сжимаемости грунта m ₀:

m ₀ = tga (2.3)

или в дифференциальной форме

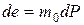, . (2.4)

Это выражение может быть сформулировано следующим образом: бесконечно малое изменение объема пор прямо пропорционально изменению внешнего давления.

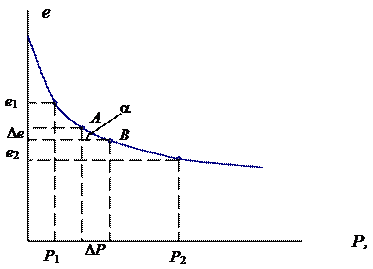
Рис.2.8. Определение параметров отрезка компрессионной кривой

При небольших изменениях внешнего давления 0,1…0,3 МПа этот закон можно распространить и на конечные изменения величин P и e:

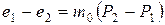, (2.5)

откуда

или при

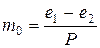, (2.6)

т.е. коэффициент сжимаемости равен отношению изменения коэффициента пористости к величине действующего давления.

Из компрессионной кривой находим

e_i = e ₀ – m ₀ P_i. (2.7)

При расчетах осадок обычно пользуются так называемым коэффициентом относительной сжимаемости m _n

. (2.8)

Физический смысл этого коэффициента устанавливаем из соотношения

e ₀ - e_i = m ₀ P_i.

С другой стороны, из выражения (2.2) имеем

.

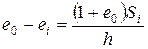Приравняем правые части этих уравнений и, принимая во внимание (2.8), получим, что коэффициент относительной сжимаемости равен относительной осадке , приходящейся на величину действующего давления:

. (2.9)

Закон уплотнения (2.9) аналогичен закону Гука, т.к. оба закона выражают пропорциональность между деформациями и вызывающими их напряжениями. Коэффициент уплотнения грунта m ₀ аналогичен обратной величине модуля нормальной упругости E.

Коэффициент уплотнения – важная расчетная характеристика грунта, дающая возможность определить величину осадок сооружений. Величину коэффициента уплотнения используют как количественную характеристику сжимаемости грунтов. Значения коэффициентов уплотнения переменны даже для одного и того же грунта, так как они уменьшаются с увеличением давления (соответственно и с увеличением плотности грунта).

При некоторых средних по величине давлениях порядка 0,2¸0,3 МПа грунты по сжимаемости можно различать следующим образом:

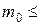0,0005 1/МПа – малосжимаемые;

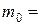0,0005-0,005 1/МПа – среднесжимаемые;

0,005 1/МПа – сильносжимаемые.

Общий случай компрессионной зависимости. Изменения коэффициента пористости грунта e при компрессионном сжатии в общем случае будут зависеть как от вертикальных нормальных напряжений s _z, так и от горизонтальных s _y и s _x.

Коэффициент пористости в любой точке грунтовой массы зависит только от суммы всех нормальных напряжений q, действующих в этой точке.

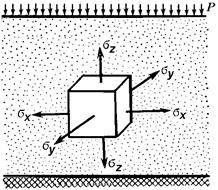Определим сумму главных напряжений в случае сжатия слоя грунта без возможности бокового расширения (рис.2.9). Так как горизонтальные деформации невозможны, то горизонтальные относительные деформации будут равны нулю: e _x = e _y = 0, откуда вытекает, что s _y =s _x из условия равновесия, s _z = P.

Рис.2.9. Схема напряжений в элементе грунта при действии сплошной равномерно распределенной нагрузки

При действии напряжений по трем взаимно перпендикулярным направлениям относительные горизонтальные деформации определяем по формуле

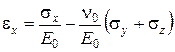, (2.10)

где E ₀ и n₀ – модули общих деформаций грунта.

Подставляя в формулу (2.10) значения s _y =s _x, s _z = P и e _x = 0, получим

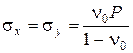(2.11)

или 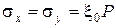, (2.12)

где коэффициент бокового давления грунта в состоянии покоя

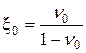, (2.13)

В рассматриваемой точке сумма главных напряжений q

q = s _x + s _y + s _z. (2.14)

С учетом s_z = P и s _y = s _x = x₀ P получим

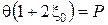, (2.15)

откуда

. (2.16)

Подставляя значение (2.16) в уравнение компрессионной кривой (2.7), получим

, (2.17)

откуда

. (2.18)

Из этого уравнения видно, что изменение коэффициента пористости грунтовой массы в рассматриваемой точке может произойти лишь при изменении суммы главных напряжений q – это “принцип гидроемкости” (по Н.М.Герсеванову).

Дата добавления: 2014-01-07