Изохорный процесс

1. Этот термодинамический процесс имеет место в тех случаях, когда объем газа во время всего процесса остается неизменным;

2. V = const - уравнение процесса.

	P

- семейство изохор.

V

Семейство изохор - семейство параллельных линий.

Чем ближе к оси ОР, тем меньше удельный объем V (м³/кг).

3. Уравнение состояния в крайних' точках любого изохорного процесса 1-2 будут выглядеть так:

В т. 1 ;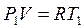

В т. 2 ;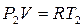

;

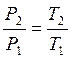В изохорном процессе давление газа пропорционально абсолютной температуре.

Процесс 1-2 - идет с увеличением температуры, а 2-1 - с уменьшением.

4. Изменение внутренней энергии :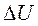

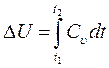
Для идеального газа C_v – const

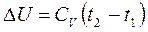
5.Работа в изохорном процессе равна О:

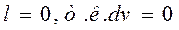
6. Согласно первому закону термодинамики, теплота, подводимая в изохорном процессе, будет идти полностью на увеличение внутренней энергии:

Изобарный процесс

1. Термодинамический процесс, протекающий при постоянном давлении Р = const - называется изобарным.

2. В координатах PV-линии II оси абсцисс:

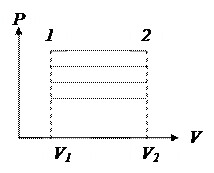3. Для изобарного процесса уравнение состояния идеального газа

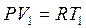
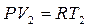
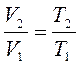
Объемы газов пропорциональны абсолютным температурам.

4. Изменение внутренней энергии :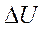

;

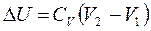5. Работа в изобарном процессе:

или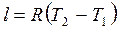

Из последнего выражения для работы легко установить физический смысл газовой постоянной R, если изменение температуры в изобарном процессе будет равно 1 градусу, то R = 1.

Газовая постоянная есть работа, производимая в изобарном процессе 1 кг газа (или 1 кг газа) при изменении его температуры на 1 градус.

6. Теплота, сообщаемая газу в изобарном процессе, будет складываться согласно первому началу термодинамики из изменения внутренней энергии и работы:

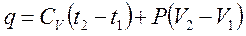
или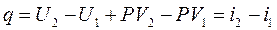

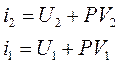
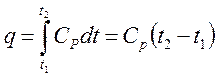
Изотермический процесс

1. Изотермическим называется процесс, осуществляемый при постоянной температуре. Согласно уравнению состояния идеального газа PV = RT, уравнение изотермического процесса выразится постоянством выражения. PV = const -уравнение состояния.

2. В координатах PV изотерма - равнобокая гипербола, т.к. в изотермическом процессе давление обратно-пропорционально объему:

1-2 изотермическое расширение;

2-1 изотермическое сжатие;

3. Связь между параметрами Т = const:

;

;

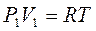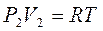
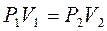
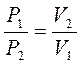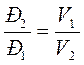
4. Внутренняя энергия остаётся неизменной, поскольку dТ=0;

5. Работа в изотермическом процессе:

;

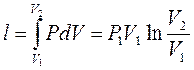т.к. давление в любой точке: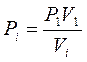

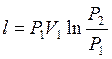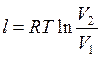или , или , или ;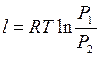

6. Поскольку изменений внутренней энергии в изотермическом процессе не происходит, то согласно первому закону термодинамики подведенная теплота будет эквивалентна работе расширения газа q = 1 (процесс 1-2 см. рис.). При сжатии газа от него должна отводиться теплота.

Адиабатный процесс

1. Термодинамический процесс, который совершается рабочим телом без теплообмена с окружающей средой, называется адиабатным. Этот термодинамический процесс объединяет все газовые процессы, которые производятся без отвода и подвода теплоты, т.е. dq = 0. Уравнение адиабатного процесса можно получить, исходя из первого начала термодинамики, из которого при dq = 0 следует, что:

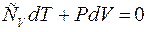
подставляем в данное уравнение выражение dT через Р и V:

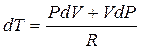
Формула Майера:

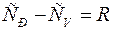
С учётом формулы Майера и элементарных преобразований:

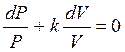
где - показатель адиабаты после интегрирования уравнения.

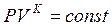
Это уравнение еще называется уравнением Пуассона или адиабатой Пуассона.

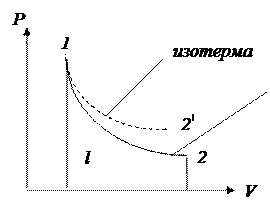
2. Графически адиабатный процесс изображается в виде несимметричной гиперболы в координатах Р – V:

Адиабата круче изотермы, т.к 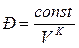, где К > 1.

3. Связь между основными параметрами:

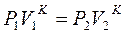
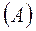
т.к. и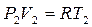

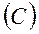
то ;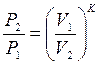

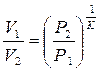или 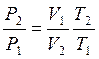, приравнивая правые части получим:

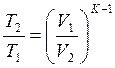по давлению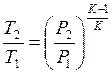

4. Изменение внутренней энергии:

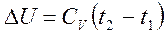
5. Если Р₁ и V₁ заданные начальные параметры адиабатного процесса, то давление Р в любой точке процесса будет связано с текущим объемом V следующей зависимостью:

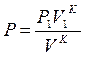
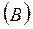
Работа газа в адиабатном процессе будет, с учетом равенства А и В:

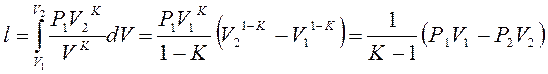
С учётом (С):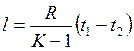

6. Теплота в адиабатном процессе не подводится и не отводится, согласно определению процесса dq = 0, но это не значит, что q = const, поскольку q - функция процесса. Запись dq = 0 надо понимать так: в адиабатном процессе не происходит теплообмена с окружающей средой.

При адиабатном расширении, в соответствии с первым законом термодинамики, работа расширения будет производиться за счет уменьшения внутренней энергии газа, т.е. 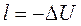, а при адиабатном сжатии газа производимая над газом работа будет эквивалента увеличению его внутренней энергии, т.е. .

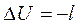Политропный процесс

В рассмотренных выше процессах один из параметров состояния сохранялся неизменным и эти процессы часто встречаются (например...).

Общим случаем термодинамического процесса является процесс со всевозможным изменением всех характеристик рабочего тела, такой процесс называется политропным (poly - много; tropos - поворот).

1. Уравнение политропного процесса получим исходя из первого начала термодинамики:

;

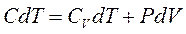dq = CdT - элементарное количество теплоты, подводимого (отводимого) в любом процессе.

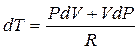с учётом формулы Майера для R.

- проведя преобразования:

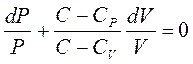, где ;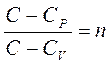

При постоянном значении истинной теплоемкости С величина n будет также постоянной.

Т.к. любой термодинамический процесс характеризуется вполне определенным постоянным значением теплоемкости С, то при интегрировании уравнения величину n - можно считать постоянной, что даст нам выражение:

;

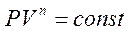Единственным ограничением политропного процесса является постоянство теплоемкости в этом процессе.

Т.к. С в газовых процессах меняется от 0 до 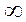, то и n изменяется от 0 до .

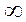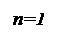
Все выше рассмотренные процессы являются частным случаем политропного процесса, если n = 0, то Р = const, если n=1, то Т=const, если n=k, то dq=0, если n=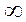, то V=const

3. В системе Р - V координат:

а). 1 > n > 0 - изобара – изотерма;

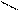
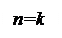
б). k > n >1 - изотерма – адиабата;

в). 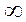> n > k - адиабата – изохора;

Политропы, идущие вправо от т. А - соответствуют случаю расширения газа, а влево от точки А - соответствуют случаю сжатия газа.

Показатель n может указывать на процесс энергопревращений:

Так 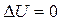при n=1, Т=const.

В политропах, лежащих над изотермой внутренняя энергия увеличивается, т.е. ;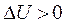

В политропах под изотермой внутренняя энергия уменьшается, т.е. ;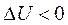

В политропах над адиабатой теплота подводится dq>0, под адиабатой соответственно отводится.

В процессах (1>n>0) подводимая теплота идет на увеличение внутренней энергии и на совершение работы расширения.

В случае сжатия - идет уменьшение внутренней энергии и отвод теплоты.

В процессах (k>n>l) - расширение газа за счет подводимой теплоты (dq>0) и уменьшения внутренней энергии ;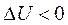

Сжатие газа сопровождается увеличением внутренней энергии 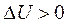и отводом теплоты (dq<0).

В процессах 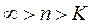- расширение газа и отвод теплоты будут происходить за счет уменьшения внутренней энергии газа (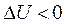), а сжатие газа и подвод теплоты сопровождаются увеличением внутренней энергии.

Качественные особенности таких энергопревращений подтверждаются зависимостью теплоемкости С от величины n:

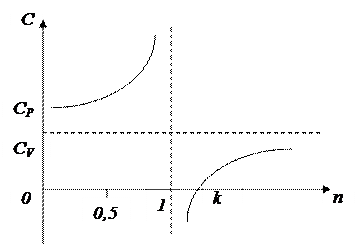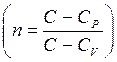
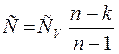
1. При n=0, теплоемкость соответствует изобарному процессу С = С_р;

1>n>0: С>0, dq>0, U>0;

2. При n=1 С стремится к бесконечности;

3. При k>n>l С - имеет отрицательные значения;

4. При n=k C=0

5. При 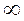>n>k C>0

6. При n=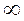C=C_V
Определим n:

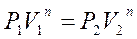
Значения Р и V в уравнение могут вводиться как координаты точек (1) и (2) без учета их масштаба (т.е. величины соответствующих отрезков).

3. Определение связи между основными параметрами состояния производится следующим образом:

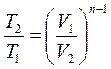
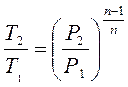
4. Изменение внутренней энергии:

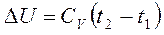
5. Формулы для вычисления работы будут аналогичны формулам адиабатного процесса, только вместо К будет n:

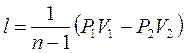
6. Тепловая энергия в политропном процессе вычисляется по зависимости:

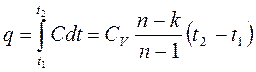
Политропным называется процесс, в котором превращение энергии осуществляется по определенному закону, т.е. процесс, в котором 1/q или 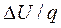имеют вполне определенные числовые значения.

Дата добавления: 2014-01-07