Для плоской задачи формула имеет вид

, (3.36)

где y – расстояние по горизонтали от середины фундамента до рассматриваемой точки; b ₁ – полуширина фундамента.

Согласно уравнениям (3.35), (3.36) по краям площадки напряжения имеют бесконечно большую величину, но поскольку грунт не может выдержать весьма больших нагрузок, близ края штампа возникают пластические деформации, за счет которых происходит перераспределение напряжений, приводящее к уменьшению напряжений по краям подошвы штампа. Эпюра распределения напряжений по подошве штампа приобретает седловидное очертание, характерное для всех без исключения грунтов, и сохраняется до тех пор, пока среднее давление на подошву штампа не превысит некоторого критического давления, при котором начинаются пластические деформации выжимания грунта из-под штампа в стороны (рис.3.26).

Рис.3.26. Распределение давлений по подошве жесткого штампа:

1 – для упругого тела;

2 – с учетом пластических деформаций

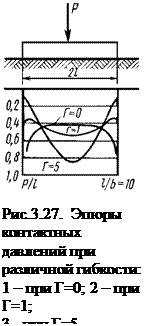Для подошвы фундаментов эпюры контактных давлений по полученным решениям, изложенным в курсе сопротивления материалов, будут прямолинейной формы – равномерной или трапецеидальной, по строгому решению теории упругости для абсолютно жестких фундаментов они всегда седлообразные, а для фундаментов конечной жесткости эпюра принимает очертание от седлообразного до параболического (рис.3.27) в зависимости от гибкости фундамента Г. Критерием оценки жесткости фундамента может служить показатель гибкости по М.И.Горбунову-Посадову

,

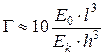где E ₀ и E_k – модули деформации грунта основания и материала конструкции; l и h – длина и толщина конструкции. Если Г=0, конструкция абсолютно жесткая.

На рис.3.27 показано три кривых распределения контактных давлений в зависимости от гибкости фундамента. Следует отметить, что распределение контактных давлений по подошве фундамента зависит от глубины заложения, величины внешней нагрузки и других факторов.

3.8. Распределение напряжений в грунте от нагрузки, приложенной внутри массива

Нагрузка от свайных фундаментов и опор глубокого заложения действует внутри массива. При расчете полных осадок и осадок во времени, учете взаимного влияния фундаментов, оценке прочности грунтов, проверке напряжений в слое грунта, более слабом по несущей способности, чем вышележащие слои, необходимо знать и учитывать распределение напряжений в массиве под свайными фундаментами и на различном расстоянии от него во всей активной зоне. В работе [6] приведены решения пространственной и плоской задач для определения напряжений по оси куста свай и ленточных свайных фундаментов, а также решение краевых задач для определения напряжений в любой точке активной зоны при центральном и внецентренном приложении нагрузки с учетом закономерностей передачи нагрузки по боковой поверхности и в плоскости острия свай, параметров фундамента, физико-механических свойств грунтов.

При решении пространственной задачи для кустов свай использована формула Р.Миндлина (1936), а при решении плоской задачи для определения напряжений в активной зоне ленточных свайных фундаментов – формула Е.Мелана (1932) для вертикальных сжимающих напряжений от ряда сосредоточенных сил Р, приложенных на глубине h.

Для практических расчетов формула для определения напряжений в активной зоне кустов свай приведена к виду

, (3.37)

где P – нагрузка на свайный фундамент; l – длина свай; – безразмерный коэффциент, табулированный в зависимости от коэффициента Пуассона, отношения сторон фундамента, относительной глубины рассматриваемой точки и расстояния рассматриваемой точки от оси, а для внецентренно загруженных фундаментов и с учетом эксцентриситета приложения нагрузки (табл.II.6, II.7, II.8, II.9 приложения II).

Для ленточных свайных фундаментов формула для определения напряжений в активной зоне имеет вид

, (3.38)

где P – нагрузка на свайный фундамент, Н/см; l – длина сваи; a₀ – безразмерный коэффициент, принимаемый по таблицам в зависимости от характера передачи нагрузки по боковой поверхности и в плоскости острия свай, приведенной ширины свайного фундамента, коэффициента бокового расширения грунта (табл.II.10, II.11 приложения II).

Дата добавления: 2014-01-07