Аддитивная модель временного ряда

Рассмотрим процедуру построения аддитивной модели временного ряда на следующем примере.

Имеются данные об объеме потребления электроэнергии за 4 года:

Квартал Год	I	II	III	IV

Если нанести данные за 16 кварталов на график, то можно убедиться, что исследуемый временной ряд содержит сезонные колебания приблизительно равной амплитуды с периодичностью 4. Для такого ряда можно построить аддитивную модель. Рассчитаем ее компоненты.

Шаг 1. Проведем выравнивание уровней ряда методом скользящей средней:

а) последовательно просуммируем уровни ряда по четыре со сдвигом на один момент времени;

б) найдем скользящие средние, разделив полученные суммы на 4;

в) привяжем полученные средние значения к фактическим моментам времени t. Для этого найдем средние значения для каждых двух последовательных скользящих средних, т.е. определим центрированные скользящие средние. Результаты занесем в таблицу 1: Таблица 1

T		Итого за 4 квартала	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
		- -	- 67,5 77,5 82,5 83,5 -	-
		-
		62,5	-12,5
		64,5	25,5
		66,25	5,75
		68,75	-20,75
			-11
		74,5	5,5
		76,25	-20,25
		78,75	-14,75
		81,25	28,75
		83,25	6,75
		83,75	-17,75
		-	-
		-	-

Шаг 2. Вычислим оценки сезонной компоненты S, для чего из фактических уровней ряда вычтем значения центрированных скользящих средних. Результаты занесем в последний столбец табл.1. Найденные оценки используем для расчета значений сезонной компоненты S. Для этого найдем средние значения оценки сезонной компоненты 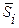за каждый i -й квартал (по всем 4 годам):

Таблица 2

Показатель	Год	№ квартала, I
I	II	III	IV
		- 5,75 5,5 6,75	- -20,75 -20,25 -17,75	-12,5 -11 -14,75 -	25,5 28,75 -
Итого за i -й квартал			-58,75	-38,25	81,25
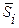
			-19,58	-12,75	27,08
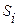
		5,813	-19,77	-12,94	26,89

Используя рассчитанные значения 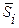, определим корректирующий коэффициент k:

и вычислим скорректированные значения сезонной компоненты 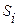для каждого квартала (последняя строка табл. 2):

.

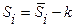Проверим условие равенства нулю суммы значений :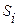

: 5,813 - 19,77 - 12,94 + 26,89 = 0.

Занесем найденные значения 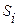в таблицу 3 (столбец 3) для соответствующих кварталов каждого из 4 лет.

Шаг 3. Из исходных уровней ряда удалим значения сезонной компоненты S, найденные на шаге 2, т.е. получим выровненные уровни = Y – S (заполним столбец 4 табл.3).

Шаг 4. Определим трендовую компоненту T данной модели. Для этого выполним аналитическое выравнивание ряда () с помощью линейной функции 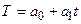. Коэффициенты линейного уравнения трендовой компоненты вычислим обычным МНК. В качестве значений независимой переменной t используем номера кварталов (столбец 1 табл. 3), а в качестве значений зависимой переменной Т – значения выровненных уровней (столбец 4 табл. 3). Таблица 3

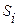
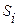
t			=-	Т	T+S	E =-(T+S)	E ^2	е^2
		5,813	54,187	59,019	64,83	-4,832	23,35	172,27
		-19,77	63,77	60,883	41,11	2,887	8,332	848,27
		-12,94	62,94	62,748	49,81	0,192	0,037	534,77
		26,89	63,11	64,612	91,5	-1,502	2,257	284,77
		5,813	66,187	66,477	72,29	-0,29	0,084	1,2656
		-19,77	67,77	68,341	48,57	-0,571	0,326	631,27
		-12,94	72,94	70,205	57,27	2,735	7,479	172,27
		26,89	73,11	72,07	98,96	1,04	1,082	722,27
		5,813	74,187	73,934	79,75	0,253	0,064	47,266
		-19,77	75,77	75,798	56,03	-0,028	0,001	293,27
		-12,94	76,94	77,663	64,72	-0,723	0,522	83,266
		26,89	83,11	79,527	106,4	3,583	12,84	1359,8
		5,813	84,187	81,391	87,2	2,796	7,816	284,77
		-19,77	85,77	83,256	63,49	2,514	6,322	50,766
		-12,94	82,94	85,12	72,18	-2,18	4,752	9,7656
		26,89	81,11	86,984	113,9	-5,874	34,51	1216,3

Построенное с использованием МНК уравнение тренда имеет вид:

.

Подставив в это уравнение значения переменной t (номера кварталов), найдем значения уровней трендовой компоненты Т для каждого из кварталов (заполним столбец 5 табл. 3).

Шаг 5. Рассчитаем значения уровней ряда, соответствующих сумме трендовой и сезонной компонент T+S. Для этого сложим значения 3-го и 5-го столбцов таблицы 3.

Шаг 6. Вычислим значение случайной компоненты (абсолютной ошибки):

,

т.е. найдем разность значений 2-го и 6-го столбцов. Для оценки качества построенной модели найдем сумму квадратов абсолютных ошибок =109,77.

Определим квадраты отклонений уровней временного ряда от его среднего уровня =73,125, т.е. заполним столбец 9 таблицы:

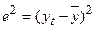
и рассчитаем общую сумму квадратов ошибки =6712,25.

Используя и , вычислим коэффициент детерминации: =0,984.

Таким образом, построенная аддитивная модель временного ряда объясняет 98,4% изменений уровней потребления электроэнергии за 4 года (16 кварталов).

Дата добавления: 2014-01-07