Имитационный алгоритмический способ

Имитационный способ представления задачи 1

Аналитический неявный способ

В данной формулировке за счёт использования знака уравнивания получена связь переменных f (T, V ₁, V ₂, D, S) = 0 в виде системы уравнений. Устанавливая знак «?» на различные переменные, можно формулировать при необходимости целый ряд произвольных задач, например так:

T₁ · (V₁ + V₂) = D
S₁ = V₁ · T₁
T₁ =?

При этом задачи формулируются пользователем и не предусматриваются специально моделировщиком. То есть модель имеет вид объекта. Мы получили более качественную модель. Идеализация её велика, но за счёт неявной формы записи появилась возможность изменения задачи, изучения на ней целого ряда проблем.

При имитационном способе решения обязательным является наличие некоего счётчика, который позволяет моделировать процесс по шагам или по деталям процесса.

Повторяя пошагово расчёт в цикле, на каждом этапе работы алгоритма будем имитировать течение процесса (рис. 1.19). Обратите внимание, что процесс берётся не в целом, а как бы в деталях, по шагам. Переменная t является координатой, а значит, отслеживается счётчиком с шагом h. Идея имитации — продвигать пешехода и велосипедиста на величину V · h на каждом такте, где h — достаточно малая величина. Поскольку мы рассматриваем множество актов движения по отдельности, можно по ходу менять все переменные модели, например, V. Если путь пройден большой (S ₁), то можно устроить привал (V = 0) на некоторое время. Остановка процесса имитации определяется суммой путей, пройденных велосипедистом и пешеходом навстречу друг другу, и сравнением её с расстоянием D.

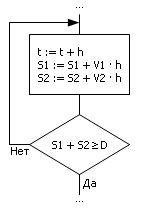
Рис. 1.19. Блок-схема решения задачи о встрече
(имитационный алгоритмический способ)

На формально-математическом языке алгоритм выглядит так, как показано ниже.

t:= t + h · e
S₁:= S₁ + V₁ · h · e
S₂:= S₂ + V₂ · h · e
e:= ed(D – (S₁ + S₂))
f:= not(e)
stop(f)

e — вспомогательный флаг;
f — флаг, показывающий, был ли пройден к текущему моменту t весь путь или нет;
ed(x) — единичная функция: ed(x) = 1 при x ≥ 0, иначе ed(x) = 0;
stop(z) — функция останова вычислений при z > 0.

Дата добавления: 2014-01-07