Основні означення та поняття

Звичайні диференциальні рівнянняя.

Def. 1 Рівняння, що містить невідому (шукану) функцію під знаком диференціала або похідної, називається диференціальним (ДР).

Def. 2 Диференціальне рівняння, що містить невідому (шукану) функцію, що залежить тільки від однієї змінної, називається звичайним.

Def. 3 Порядком ДР називається порядок старшої похідної або диференціала, котрий фігурує в даному ДР.

Приклад 1 ДР 2-го порядку:

.

Таким чином, загальним виглядом диференціального рівняння п -го порядка 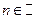являється рівняння вигляду:

, (1)

де F – задана функція.

Def. 4 Якщо рівняння (1) можна представити у вигляді:

, (2)

то кажуть, что ДР задано відносно старшої похідної.

Def. 5 Процес знаходження розв’язку данного ДР називається інтегруванням ДР.

Def. 6 Інтегралом (розв’язком) ДР (1) на інтерваліназивається така n разів диференційована на проміжку функція, яка при підстановці в ДР (1) перетворює його у вірну рівність:

Def. 7 Множина всіх розв’язків ДР називається загальним інтегралом (загальним розв’язком) ДР:

.

Якщо всі розв’язки ДР задаються у явному вигляді:

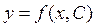
то використовується термін «загальний розв’язок».

Def. 8 Початковими умовами ДР (1) називаються вирази вигляду:

, (3)

що задаються в одній точці , де 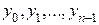задані числа.

Def. 9 Краєвими умовами для ДР (1) називаються вирази, які задають значення шуканої фунції і/або її похідних до порядку (n -1) включно в різних точках x_k .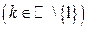

Def. 10. Розв’язком задачі Коші для ДР (1) називається виокремлення частинного розв’язку із загального розв’язку ДР (1) з використанням початкових умов.

Теорема 1 (Про існування та єдності розв’язку) Нехай в області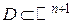

(D – область інтегрування ДР (2)) функція являється неперервною разом зі своїми частинними похідними за сукупністю змінних . Тоді при любих початкових значеннях, т.б. точок вигляду 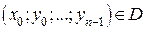, ДР (2) має єдиний розв’язок, визначений на деякому інтервалі 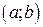(), який задовольняє початковим умовам вигляду (3).

Дата добавления: 2014-01-07