
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энергия заряженного конденсатора
|
|
|
|
Заряженный конденсатор обладает энергией, возникающей в процессе зарядки конденсатора. Это потенциальная энергия взаимодействия разноименно заряженных обкладок конденсатора. Если одну из пластин плоского конденсатора предоставить саму себе, то она под действием силы поля второй пластины будет к ней притягиваться, увеличивая скорость и, как следствие, свою кинетическую энергию. В момент соприкосновения пластин конденсатора вся потенциальная энергия перейдет в кинетическую, а после – во внутреннюю, нагревая пластины. Первая пластина конденсатора, в таком случае, приближается ко второй за счет работы, которую совершает поле второй пластины.
Выразим величину силы, с которой электрическое поле второй пластины притягивает к себе первую (при этом будем считать, что вторая пластина конденсатора заряжена отрицательно, а первая – положительно).
Из определения напряженности электростатического поля следует, что: 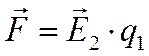 .
.
Избавляясь от векторов, получим:  .
.
 – это напряженность поля второй пластины.
– это напряженность поля второй пластины.
Для заряженной бесконечной плоскости  .
.
Здесь  – поверхностная плотность заряда второй пластины.
– поверхностная плотность заряда второй пластины.
Тогда 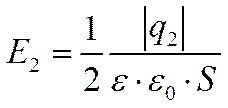 , а
, а 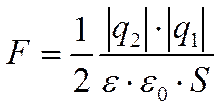
Учитывая, что заряды обеих пластин конденсатора одинаковые, и их абсолютные значения называются зарядом конденсатора
(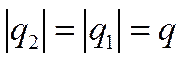 где
где  – это заряд конденсатора), то
– это заряд конденсатора), то
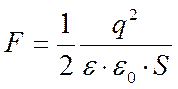
Вычислим работу постоянной силы, с которой поле второй пластины конденсатора притягивает к себе первую пластину:
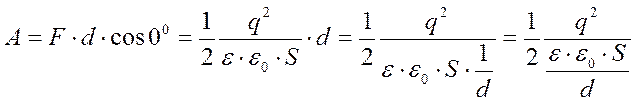 .
.
Учитывая, что электроемкость плоского конденсатора выражается по формуле  , получаем:
, получаем:

|
Также работа равна убыли потенциальной энергии:

Так как кинетическая энергия первой пластины принимает свое максимальное значение в момент соприкосновения пластин, то потенциальную энергию взаимодействия пластин в этот момент времени можно считать равной нулю 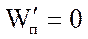 .
.
Тогда 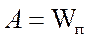 или или
| 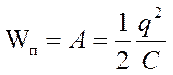
| 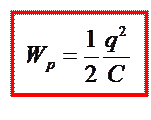
|
Используя определение электроемкости конденсатора,
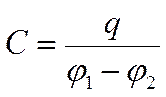 получим, что получим, что
| 
|
| или | 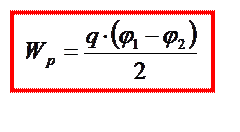
|
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 485; Нарушение авторских прав?; Мы поможем в написании вашей работы!