Сутність регресійного аналізу

План

1. Сутність регресійного аналізу.

2. Оцінка параметрів парної лінійної регресії методом найменших квадратів (МНК). Властивості МНК- оцінок.

3. Коефіцієнти кореляції та детермінації.

4. Перевірка моделі на адекватність за критерієм Фішера.

Однією з головних задач економетрії в ринковій економіці є ретельне вивчення кількісних зв’язків між показниками для кращого розуміння господарських явищ і процесів, що в свою чергу дозволяє більш обґрунтовано сформулювати управлінське рішення та дати прогнози на майбутнє. Для вирішення цієї задачі потрібно вміти будувати економетричні моделі.

Зв’язок між різними явищами в економіці складний і різноманітний. На рівень розвитку одного показника можуть впливати багато факторів, рівень впливу яких різний. Ці закономірності потрібно враховувати під час планування, прогнозування і проведення економічного аналізу.

Для вивчення форми зв’язку між показником і факторами на основі статистичних даних використовується регресійний аналіз. Причому, об’єктами дослідження стохастичної залежності соціально – економічних процесів можуть бути різні статистичні показники.

Статистичний показник – узагальнена характеристика певної властивості сукупності, групи.

Наведемо приклади статистичних показників в економіці: обсяг реалізованої продукції; собівартість продукції; прибуток підприємства; суспільний продукт і т.д.

Описати стохастичні залежності між економічними показниками можна за допомогою кореляційно - регресійного аналізу.

Задачею регресійного аналізу є встановлення виду залежностей між змінними та вивчення залежності між ними. Основною задачею кореляційного аналізу є виявлення зв’язку між змінними та оцінка її тісноти та значимості.

Але на застосування кореляційно – регресійного аналізу накладаються такі вимоги:

1. необхідність достатньо великої сукупності спостережень;

2. забезпечення однорідної сукупності спостережень;

3. наявність нормального закону розподілення в сукупності значень показників.

Модель, що описує кореляційно-регресійний зв'язок між економічними показниками називається загальною, яка дійсна для всієї генеральної сукупності спостережень.

У лінійній економетричній моделі має місце лінійний зв'язок між змінними, що характеризують певний економічний процес чи явище. Зауважимо, що лінійні регресійні моделі є найбільш простою, і в переважній більшості випадків - достатньою для практики. Ті з моделей, що використовують метод найменших квадратів (МНК) при оцінці параметрів, називаються класичними і вивчаються у класичній економетрії.

Розглянемо економетричну модель представлену загальною лінійною регресією вигляд якої наступний: 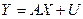, (1)

Де - матриця значень залежної змінної (пояснювальної змінної);

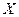- матриця значень незалежних змінних (пояснюючих змінних);

- матриця параметрів моделі розмірністю 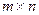(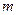- кількість незалежних змінних, - число спостережень);

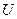- матриця випадкової складової.

Незалежні змінні Х (пояснюючі змінні) найчастіше бувають детерміністичними і вони є наперед заданими змінними, або вхідними показниками для економетричної моделі.

Випадкові складові 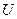називаються стохастичними складовими, помилками, залишками. Вони є наслідками помилок спостережень, містять у собі вплив усіх випадкових факторів, а також факторів, які не входять у модель.

Залежні змінні (пояснювальні змінні) є результативними показниками, які залежать від факторів 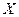та випадкової складової 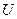. Отже, вони також є стохастичними, тобто випадковими. Тому, економетрична модель є стохастичною.

Розглянемо найпростіший вид лінійної регресії: парна лінійна регресійна модель (лінійна однофакторна регресія).

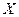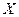Парною лінійною регресією на називається одностороння стохастична лінійна залежність між випадковими величинами показника і одного фактора , які знаходяться в причинно – наслідкових відношеннях, причому зміна фактора виключає зміну показника.

Загальний вигляд лінійної однофакторної регресії наступний:

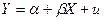, (2)

Де - залежна змінна (пояснювальна змінна);

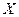- незалежна змінна (пояснююча змінна);

- параметри моделі;

- випадкова складова.

Регресія характеризує тенденцію зміни статистичного показника зумовлену впливом зміни фактора 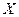. Позначимо оцінки параметрів регресії через . В результаті отримаємо рівняння парної лінійної регресії: . Вона вважається побудованою, якщо визначені .

2.Оцінка параметрів парної лінійної регресії методом найменших квадратів (МНК). Властивості МНК- оцінок.

Для оцінки параметрів регресії використаємо метод найменших квадратів (1 МНК).

Зауваження: Основоположниками методу є математики К. Гаус і П. Лаплас.

Суть методу МНК: Оцінки параметрів моделі мають бути такими, щоб мінімізувати суму квадратів залишків кожного спостереження показника, тобто .

Параметри регресії можна визначити із нормальної системи рівнянь:

(3)

Розв’язавши лінійну систему отримаємо параметри .

Для знаходження оцінок параметрів лінійної однофакторної регресії можна використати функцію «ЛИНЕЙН» в Excel.

Властивості методу МНК.

1. МНК-оцінки є лінійними комбінаціями спостережень .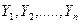

2. Відхилення МНК-оцінок від істинних значень відповідних параметрів є лінійними комбінаціями помилок

3. В регресійній моделі МНК- оцінки є не зсуненими оцінками відповідних параметрів .

4. (теорема Гауса - Маркова). Із усіх можливих лінійних не зсунених оцінок параметрів регресійної моделі тільки МНК – оцінки є найкращими лінійними не зсуненими оцінками.

5. МНК – оцінки регресійної моделі є обґрунтованими.

Дата добавления: 2014-01-07