
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кількісні методи опрацювання експертних оцінок
|
|
|
|
Фактори впливу на експерта
У діяльності експертів дуже важливу роль грають фактори психологічного характеру та ще так звані „фактори впливу” на їх висновки. Перш за усе експерти мають бути звільнені від відповідальності за використання результату експертизи. Сама відповідальність накладає психологічні обмеження на характер вибору, а цього на етапі оцінки альтернатив бажано уникати. Доводиться також враховувати, що оцінка експерта може залежати від між особових стосунків із другими експертами та іноді навіть від того, чи відома його оцінка другим особам. На хід експертизи можуть впливати й особова зацікавленість експерта, тобто його необ’єктивність, і власні якості (самолюбивість, конформізм, сила характеру тощо). З другого боку, зазвичай складність проблеми виходить за рамки можливостей однієї людини. Було б нерозумно ігнорувати очевидний факт, що колективна діяльність відкриває додаткові можливості для взаємного стимулювання експертів.
Оскільки взаємодія між експертами може як стимулювати, так й подавляти їх діяльність, у різних випадках використовують методики експертиз, що мають різні ступені та характер взаємного впливу експертів один на одного: анонімні та відкриті опитування, анкетування, наради (комітети, колегії, комісії, штаби), дискусії (консиліуми, суди, вчені ради), ділові ігри, мозковий штурм тощо.
Розглянемо проблему вибору на основі експертних оцінок з точки зору академіка В.М. Глушкова, який розглядав системний аналіз як сукупність прийомів та методів дослідження складних об’єктів, котрим дав термін „ узагальнені динамічні системи ”. Узагальнена динамічна система являє собою сукупність взаємозв’язаних об’єктів та процесів, що змінюються у часі. Прикладами таких систем можуть бути сонячна система, людський організм, промислове підприємство, економіка окремої або групи країн тощо.
Розглянемо більш докладніше два класи моделей узагальнених динамічних систем, які називаються відповідно булевими моделями з односторонніми та із двосторонніми переходами. Моделі є булевими тому, що усі характеризуючи їх параметри (включаючи елементарні зовнішні впливи) являються булевими. У першій моделі спочатку усі параметри мають значення 0 та у деякі моменти часу (різні для різних параметрів) можуть змінити це значення на 1, після чого їх зворотний перехід виявляється неможливим.
Саме у цьому полягає якість односторонніх переходів, що відмічено в назві моделі. У моделі із двосторонніми переходами параметри можуть довільне число разів змінювати свої значення з 0 на 1 та зворотно.
Для з’ясування сутності моделі, розглянемо її у конкретній інтерпретації – як задачі прогнозування науково-технічного прогресу. Припустимо, що вимагається оцінити час та шляхи рішення деякого числа нерозв’язаних сьогодні науково-технічних проблем s 1, s 2,..., s m. Серед них можуть бути як проблеми суттєво прикладного характеру (наприклад, проблема підвищення продуктивності праці у вугільній промисловості у 10 разів), так й абстрактні проблеми (наприклад, побудову єдиної теорії поля). Припустимо далі, що кожній згаданій проблемі s i приписаний деякий ваговий коефіцієнт λ ί, що визначає відносну важливість проблеми порівняно із іншими (і = 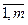 ). Поставимо в якості мети розв’язок всіх вказаних проблем, а в якості критерію якості керування – мінімізацію суми Σλ ί τ ί, де τ ί - строк, що вимагається для вирішення проблеми s i при заданих сумарних ресурсах R, відпущених на рішення усіх цих проблем.
). Поставимо в якості мети розв’язок всіх вказаних проблем, а в якості критерію якості керування – мінімізацію суми Σλ ί τ ί, де τ ί - строк, що вимагається для вирішення проблеми s i при заданих сумарних ресурсах R, відпущених на рішення усіх цих проблем.
Початкова структуризація проблеми полягає у тому, щоби доповнити список поставлених проблем (назвемо їх конечними або основними цілями) s 1, s 2,..., s m новими проблемами (проміжними цілями) s m+1,..., s m+n, розв’язок котрих може з’явитися необхідним для досягнення конечних цілей. Параметризація полягає у приписувані кожному виділеному елементу двох булевих параметрів α ί(t) та β ί(t), (i =  ). Перший характеризує стан елементу (проблема s i розв’язана чи ні), а другий – керуючий вплив (проблема s i включена у план та фінансується або ні). Введемо оцінку імовірності P i(t) того, що до часу t проблема буде розв’язаною, тобто імовірність того, що α ί(t) = 1, (i =
). Перший характеризує стан елементу (проблема s i розв’язана чи ні), а другий – керуючий вплив (проблема s i включена у план та фінансується або ні). Введемо оцінку імовірності P i(t) того, що до часу t проблема буде розв’язаною, тобто імовірність того, що α ί(t) = 1, (i =  ).
).
З метою виявлення залежності між параметрами для кожної із проблем s i залучається група експертів. Кожний експерт формулює умову, що полягає у тому, чи деякі цілі s i1, s i2,..., s ik вважаються вже досягнутими, і дає оцінки часу t i досягнення цілі s i після виконання поставленої умови. Ця оцінка може виконуватися для декількох різних величин асигнованій v i, необхідних для розв’язку проблеми s i, так що t i являються в загальному випадку функцією від v i. У результаті виникають залежності між параметрами α i виду:
α i(t) = α i1(t - t i) α i2(t - ti)… α ik(t - t i). (1)
Для довільного заданого і буде декілька таких залежностей у відповідності з числом експертів. Кожна залежність отримує ваговий коефіцієнт r ij (і – номер цілі; j - номер експерта в групі). Із залежностей виду (1), що установлені різними експертами, отримують наступну очевидну формулу для обчислення імовірності:
P i(t) =  (2)
(2)
де через ij 1 ,ij 2,..., ijkj позначені номери проміжних цілей, висунутих j –м експертом як умову досягнення мети s i; а t ij - оцінка часу досягнення цілі s i після виконання поставленої умови.
Для того, щоби по рівнянням виду (2) можна було послідовно знайти функції P i(t) для всіх цілей s i, (i =  ), потрібно у процесі побудови моделі виконати деякі додаткові уточнення. Одне полягає у тому, що, вводячи нові допоміжні цілі та додатково працюючи із експертами, добиваються розбиття множини всіх цілей (як конечних, так й допоміжних) на непересічні підмножини М 0, М 1,..., М р. Множина М 0 складається із цілей, що мають лише безумовні оцінки часу свого досягнення. Для цілей у довільній із множин М і в якості умов можуть виступати цілі із множин М 0, М 1,..., М і-1, (і =
), потрібно у процесі побудови моделі виконати деякі додаткові уточнення. Одне полягає у тому, що, вводячи нові допоміжні цілі та додатково працюючи із експертами, добиваються розбиття множини всіх цілей (як конечних, так й допоміжних) на непересічні підмножини М 0, М 1,..., М р. Множина М 0 складається із цілей, що мають лише безумовні оцінки часу свого досягнення. Для цілей у довільній із множин М і в якості умов можуть виступати цілі із множин М 0, М 1,..., М і-1, (і =  ). При виконанні цієї вимоги формула (2) виявляється достатньою для обчислення ймовірностей P i(t) для всіх цілей при всіх значеннях t (з деяким інтервалом дискретності).
). При виконанні цієї вимоги формула (2) виявляється достатньою для обчислення ймовірностей P i(t) для всіх цілей при всіх значеннях t (з деяким інтервалом дискретності).
Для з’ясування смислу таких обчислень, розглянемо простіший прилад. Нехай задані дві конечні цілі s 1 та s 2 з вагами 2 та 1 відповідно та дві допоміжні цілі s 3 та s 4, кожна з котрих оцінювалася двома експертами. Дані оцінок зведені у наступній таблиці (для простоти нехтуємо залежністю оцінок часу t ij від розміру виділених асигнованій).
| Цілі | s1 | s2 | s3 | s4 | ||||
| Експерти | ||||||||
| Умовні | (s2, s4) | (s3, s4) | (s3, s4) | (s2) | (s2) | - | - | - |
| Оцінка часу tij | ||||||||
| Вага rij |
З таблиці безпосередньо видно, що цілі розпадаються на шари М 0 (ціль s 4), М 1 (ціль s 3), М 2 (ціль s 2), М 3 (ціль s 1). Функції P i(t) будемо задавати векторами Р і( 0 ); Р і( 1 ); Р і( 3 );... Починаючи з деякого t,усі P i(t) у цих векторах дорівнюють 1 і у цих місцях вектори будуть обірвані (недостатні компоненти при необхідності можуть бути дописаними). Якщо експерт не висунув жодних умов, то добуток r ij P ij1 (t – t ij)… P ijkj (t – tij) у рівняннях (2) мусить бути заміненим на r ij Q (t – t ij), де Q (t) = 0 при t ≤ 0 та Q (t) = 1 при t ≥ 0.
У такому випадку отримаємо наступне:
P 4(t) =  Q (t – 2 ) +
Q (t – 2 ) +  Q (t – 3 ) =
Q (t – 3 ) =  ( 0; 0; 1; 1 ) +
( 0; 0; 1; 1 ) +  ( 0; 0; 0; 1 ) = ( 0;0;0,6;1 );
( 0; 0; 0; 1 ) = ( 0;0;0,6;1 );
P 3(t) =  Q (t – 2 ) +
Q (t – 2 ) +  P 4(t - 1 ) =
P 4(t - 1 ) =  ( 0; 0; 1; 1; 1 ) +
( 0; 0; 1; 1; 1 ) +  ( 0; 0; 0;.6; 1 ) =
( 0; 0; 0;.6; 1 ) =
= ( 0; 0;.75;.9; 1 );
P 2(t) =  P 3(t - 2 ) P 4(t - 2 ) +
P 3(t - 2 ) P 4(t - 2 ) +  P 3(t - 4 ) = ( 0; 0; 0; 0;0,18;.36;.85;.94; 1 );
P 3(t - 4 ) = ( 0; 0; 0; 0;0,18;.36;.85;.94; 1 );
P 1(t) =  P 2(t - 2 ) P 4(t - 2 ) +
P 2(t - 2 ) P 4(t - 2 ) +  P 3(t - 2 ) P 4(t - 3 ) = ( 0; 0; 0; 0; 0; 0;.18;.47;.61;.91;.97; 1 ).
P 3(t - 2 ) P 4(t - 3 ) = ( 0; 0; 0; 0; 0; 0;.18;.47;.61;.91;.97; 1 ).
Ці дані можуть бути використаними для прогнозу найбільш імовірного часу досягнення кожної цілі, що аналізується. Звичайно в якості такого часу прийнято вважати медіану розподілу, тобто час t, для якого імовірність P i(t) дорівнює.5. Якщо вважати, що між знайденими точками імовірність P i(t) змінюється по лінійному закону, то, як вказано для випадку P i(t) на наступному рис., медіани N i розподілів P i(t) будуть дорівнювати:
N 1 = 6 ≈ 6.21; N 2 = 5
≈ 6.21; N 2 = 5 ≈ 5.29; N 3 = 1
≈ 5.29; N 3 = 1 ≈ 1.67; N 4 = 1
≈ 1.67; N 4 = 1 ≈ 1.83.
≈ 1.83.
| P4(t) .6 .5 |  
 
| 
|   
| ||||
  
|  
|
0 1 2 3 t
Ступінь невизначеності прогнозу характеризується звичайно так званими квартилями: нижній квартиль Q i′ є значення t, при якому P i(t) =.25, а для верхнього квартиля Q ″i P (Q ″i) =.75. Легко підрахувати, що Q 4′ = 1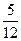 ≈ 1.42, Q 4″ = 2
≈ 1.42, Q 4″ = 2 ≈ 2.38. В якості міри невизначеності може бути вибраною різниця Q 4″ - Q 4′. Для четвертої цілі ця різниця дорівнює Δ Q 4 =
≈ 2.38. В якості міри невизначеності може бути вибраною різниця Q 4″ - Q 4′. Для четвертої цілі ця різниця дорівнює Δ Q 4 =  ≈. 96.
≈. 96.
Для уточнення прогнозу експертиза робиться неперервною: усякий раз, коли той чи інший експерт змінює свою думку, він надсилає повідомлення у систему, де відбувається перерахування функцій розподілу P i(t). Для прискорення процесу покращення прогнозу, виконується ранжирування цілей (як основних, так й проміжних) у відповідності з їх інформаційною значимістю. Найбільшою інформаційною значимістю володіють цілі, уточнення прогнозу для яких викликає найбільше уточнення для основних цілей.
Кількісною мірою інформаційної значимості i -ї цілі може бути спеціальний коефіцієнт I i, що обчислюється наступним чином. Перш за все розподіл P i(t) замінюється дельта-розподілом P ΄i(t) з тою ж самою медіаною N i (P ΄i(t) = 0 при t < N i та P ΄i(t) = 1 при t ≥ N i). Для основних цілей s 1, s 2,..., s m обчислюється зменшення d j різниць Δ Q j між відповідними квартилями (j = 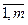 ). Тоді величину
). Тоді величину

істотно прийняти за міру інформаційної значимості i -ї цілі. Поняття інформаційної значимості допомагає концентрувати увагу експерта на цілях, уточнення прогнозу по яким є найбільш важливим. Сам процес уточнення може використовувати різні процедури додаткового звернення до експертів, цілеспрямоване постачання їх інформацією, проведення нарад із відповідними групами експертів тощо.
Близьким до поняття інформаційної значимості є поняття важливості (по строкам) тої чи іншої цілі. По визначенню коефіцієнтом важливості i –ї цілі називається величина
Z і =  ,
,
де Δi N j - прирощення медіани розподілу P j(t) при умові зсуву вправо на один часовий інтервал розподілу P i(t), тобто, іншими словами, при заміні функції P i(t) функцією P i(t - 1 ).
У розглянутому прикладі для обчислення коефіцієнта важливості Z 3 необхідно, зберігши розподіл P 4(t), замінити розподіл P 3(t) = ( 0; 0;.75;.9;1 ) на P ΄3(t) = ( 0;0;0;.75;.9;1 ).
Тоді
P ΄2(t) =  P ΄3(t - 2 ) P 4(t - 2 ) +
P ΄3(t - 2 ) P 4(t - 2 ) +  P ΄3(t - 4 ) =
P ΄3(t - 4 ) =  ( 0; 0; 0; 0; 0;.75;.9; 1 ).( 0; 0; 0; 0;.6; 1 ) + +
( 0; 0; 0; 0; 0;.75;.9; 1 ).( 0; 0; 0; 0;.6; 1 ) + +  ( 0; 0; 0; 0; 0; 0; 0;.75;.9; 1 ) = ( 0; 0; 0; 0; 0;.3;.36;.85;.94; 1 );
( 0; 0; 0; 0; 0; 0; 0;.75;.9; 1 ) = ( 0; 0; 0; 0; 0;.3;.36;.85;.94; 1 );
P ΄1(t) =  P ΄2(t - 2 ) P 4(t - 2 ) +
P ΄2(t - 2 ) P 4(t - 2 ) +  P ΄3(t - 3 ) P 4(t - 3 ) =
P ΄3(t - 3 ) P 4(t - 3 ) =  ( 0;0;0;0;0;0;0;.3;.36;.85;.94;1 ) .
( 0;0;0;0;0;0;0;.3;.36;.85;.94;1 ) .
. ( 0;0;0;0;.6;1 ) + ( 0;0;0;0;0;0;.75;.9;1 ).( 0;0;0;0;0;.6;1 ) =( 0;0;0;0;0;0;.3;.54;.62;.91;.96;1 ).
( 0;0;0;0;0;0;.75;.9;1 ).( 0;0;0;0;0;.6;1 ) =( 0;0;0;0;0;0;.3;.54;.62;.91;.96;1 ).
Звідси N ΄1 = 6 ≈ 6.83; N ΄2 = 6
≈ 6.83; N ΄2 = 6  ≈ 6.2.
≈ 6.2.
Оскільки λ 1 = 2, λ 2 = 1, то
Z 3 = 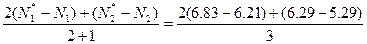 ≈.75.
≈.75.
Коефіцієнти важливості проміжних цілей можуть вживатися для вибору початкових ділянок шляхів досягнення кінцевої мети, коли прогноз ще не доведений до такого ступеня точності, щоб був можливий однозначний вибір оптимального шляху.
Легко зрозуміти, що цілі з більшим коефіцієнтом важливості являються найбільш корисними (а можливо необхідними) для досягнення кінцевої мети. Тому, коли невизначеність прогнозу ще не дозволяє вибрати оптимальні шляхи для досягнення кінцевої мети, задача управління переформулюється і тимчасовою ціллю управління може статися досягнення найбільш важливих проміжних цілей.
У більш безпосередньому вигляді така тимчасова підміна цілей може бути досягнутою введенням ваг для всіх проміжних цілей. Ці ваги позначимо через μ (s k). По визначенню
μ (s k) = 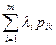 ,
,
де λ і – вага і - ї основної цілі; р ik – імовірність того, що при її досягненні виявиться необхідним попередньо досягти k –ї проміжної цілі.
Оскільки основні цілі також можуть виступати в якості проміжних (так, наприклад, ціль s 2 у розглянутому прикладі), їм можна приписати окрім вихідних базових ваг λ i також відносні ваги μ (si). Для прикладу, що розглянутий, легко отримаємо:
μ (s 1) = λ 1; μ (s 2) =. 6 λ 1 + λ 2; μ (s 3) = μ (s 4) = λ 1 + λ 2.
Керування у булевих моделях із односторонніми переходами полягає в переводі тих чи інших цілей у реальний план. Планом можна вважати й саму вихідну модель, однак, завдяки наявності у ній альтернативних шляхів довелось би досягати багатьох проміжних цілей, котрі згодом можуть виявитися непотрібними. Таким чином, смисл керування полягає у виборі альтернатив для досягнення кожної кінцевої цілі. Ці альтернативи характеризуються множинами усіх цілей, котрі треба досягти у процесі досягнення даної мети.
Підставою для вибору альтернативи служать три основні моменти. Головним являється ступінь впевненості, що дана альтернатива приведе до мети. Підставою може служити висока імовірність даної альтернативи (що залежить від числа сказаних за неї експертів) та ступінь погодженості експертів, що сказали за цю альтернативу. Мірою вказаної погодженості може бути різниця між квартилями розподілу часу досягнення мети при врахуванні тільки альтернативи, що розглядається, (із відкиданням усіх інших).
У цьому прикладі для досягнення конечної мети s 2 маємо дві альтернативи (s 3) та (s 3, s 4). Імовірність першої дорівнює, очевидно, добутку ймовірностей досягнення s 2 без s 4 та s 3 без s 4. Т обто
 .
. =
= 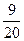 =. 45,
=. 45,
а імовірність другої – її доповненню до 1, тобто.55. Розподіл по першій альтернативі виразиться наступними функціями
P΄3 (t) = ( 0, 0, 1 ); P ΄2(t) = P ΄3(t – 4 ) = ( 0, 0, 0, 0, 0, 0, 1, 1 ).
Хоча ступінь невизначеності тут дорівнює нулю, це, розуміється, не може бути підставою для вибору першої альтернативи із огляду її невисокої імовірності.
Другою (після ступеня упевненості) підставою для вибору альтернативи служить очікуваний час (медіана розподілу P і(t)) досягнення конечної мети при відкиданні усіх інших альтернатив). Третьою підставою служить оцінка витрат для досягнення цілі s і при даній альтернативі та міра її невизначеності (середнє квадратичне відхилення або різниця між квартилями). Оцінка витрат R (s i) виконується експертами для кожної цілі s i (основної та проміжної) без включення витрат для досягнення висунутих у якості умов проміжних цілей. У цьому випадку R (s i) можна вважати незалежними випадковими величинами та оцінювати загальні витрати по кожній альтернативі сумою витрат на цілі, що входять в неї.
Виділення та оцінка альтернатив може виконуватися також для довільних груп конечних або проміжних цілей. Так, у розглянутому прикладі для групи (s 1, s 2) існує єдиний варіант (s 1, s 2, s 3, s 4), що вимагає досягнення всіх цілей, що розглядаються.
У випадку, якщо немає достатніх підстав для вибору єдиної альтернативи, для здійснення управління можна застосувати два основних прийоми. Один із них вже було розглянуто: він розуміється як включення у план найближчих цілей з найбільшими коефіцієнтами важливості (або із найбільшими відносними вагами) без наперед визначення послідовного розвитку плану. Другий прийом полягає у об’єднанні близьких альтернатив (що відрізняються невеликим числом елементів). Наприклад, альтернативи (s 1, s 3, s 5, s 6) та (s 1, s 4, s 5, s 6) можуть бути об’єднані в один варіант (s 1, s 3, s 4, s 5, s 6). Для можливості такого об’єднання суттєво, щоби цілі, котрими розрізняються об’єднувані варіанти (в даному випадку s 3 та s 4), мали порівняно невисокі витрати для їх реалізації.
Перейдемо до розгляду булевої моделі з двосторонніми переходами, яку зручно застосовувати для опису різних соціальних процесів. Знову маємо деяке число основних подій (булевих параметрів) s 1,..., s m, доповнене допоміжними подіями (параметрами) s m+1,..., s n. За допомогою експертних оцінок для кожного s i (і = 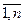 ) встановлюється залежність виду:
) встановлюється залежність виду:
s i(t) = F ij[ s ij 1(t – t ij
1(t – t ij  ),…, s i
),…, s i (t - t i
(t - t i )],
)],
де Fi j - довільна булева функція параметрів s i (що будується за допомогою логічних операцій І, АБО, НІ); t i
(що будується за допомогою логічних операцій І, АБО, НІ); t i ≥ 0.
≥ 0.
Наприклад,
s 1(t)= [ s 2(t – 1 ) s 3 (t)]
s 3 (t)]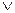 [ s 3(t – 2 )
[ s 3(t – 2 )  > s 1(t – 1 )].
> s 1(t – 1 )].
Для кожного параметра s i(t) встановлюється декілька таких залежностей (j = 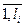 ), забезпечених вагами r ij.
), забезпечених вагами r ij.
Позначимо через p i імовірність p (s i(t)) того, що параметр s i в момент часу t мав значення 1 (подія s i мала місце). Припустимо імовірності відомими для всіх моментів минулого та теперішнього часу (t ≤ 0). Обмежуючись деякою точністю розгляду подій у часі, можна вважати, що всі часові зсуви t ijl кратні деякому елементарному проміжку часу τ. Припускаючи події у правих частинах первинних оцінок незалежними та користуючись відомими формулами
p ( s i
s i ) = 1 – p (s i
) = 1 – p (s i ); p (s i
); p (s i
 s i
s i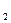 ) = p (s i
) = p (s i ) p (s i
) p (s i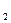 );
);
p (s i
 s i
s i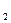 ) = 1 – p (s i
) = 1 – p (s i ) - p (s i
) - p (s i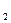 ) + p (s i
) + p (s i ) p (s i
) p (s i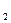 ),
),
легко підрахувати імовірність p ij(τ) настання події s i в момент часу τ у відповідності з оцінкою F ij.
Тоді імовірність p i(τ) настання події s i в момент часу τ (у відповідності з усіма наявними оцінками)
p i(τ) = 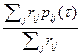 . (*)
. (*)
Послідовне повторення цього процесу призведе до обчислення ймовірностей p i(τ), p i( 2 τ ),…, p i(kτ) для всіх подій s i. Тим самим отримують прогноз розвитку моделі.
Для переходу до керування необхідно мати групу подій, поява чи не поява котрих не визначається залежностями F ij, а залежить виключно від нас (наприклад, надсилання нашої ноти у моделі відношень між державами). Назвемо ці події (параметри) керуючими і виділимо їх, вводячи нові позначення, скажемо, R 1, R 2,..., R k. Задаючи моменти настання (або не настання) цих подій, ми вносять у модель деяке управління. Залучаючи експертів для завдання тих чи інших керувань та будуючи прогноз для кожного такого керування, звичайно можна підібрати якщо не саме краще, то, в усякому разі, достатньо прийнятне керування. Роботу експертів, які задають керування, у ряді випадків доцільно організувати в інтерактивному режимі реального часу: Комп’ютер показує обстановку (значення параметрів p i(t) в даний момент часу), а експерти задають керуючі впливи R 1( t ),..., R k( t ). Далі на комп’ютері програються усі варіанти впливів, після чого (за допомогою експертів або без них) виконується вибір найкращого варіанту, а, значить, обстановки у наступний момент часу t + τ. Метою керування є досягнення обстановки із деякого класу, а критерієм є час.
Розглянемо простіший приклад булевої моделі з двосторонніми переходами.
Нехай дана основна подія s 1, одне допоміжне s 2 та одне керуюче s 3 = R. Нехай, далі, для події s 1 є дві залежності з вагами 1 та 2:
s 1(t) = [ s 1(t – 1 ) s 3(t)] s 2(t); s 1(t) = s 3(t) s 2(t).
Для події s 2 також припустимо дві залежності з вагами 2 та 1:
s 2(t) = s 1(t – 2 ) s 3(t)] s 2(t); s 1(t) = s 3(t) s 2(t).
У відповідності до наведених вище формул отримаємо:
p 1(t) =  ,
,
(**)
p 2(t) = 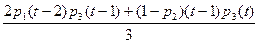 .
.
Припустимо, що задані обставини для t = -1 та t = 0. Нехай відомо, що p 3(- 1 ) = 0.
Нехай нашою метою є настання події s 1. Розглянемо два керування: p 3(t) ≡ 0 (t ≥ 0 ) та p 3(t) ≡1 (t ≥ 0 ). Користуючись формулами (**), побудуємо дві таблиці зміни обстановки у відповідності із заданими керуваннями:
| t | t | - 1 0 1 2 | |
| p1(t) | 1 0 1 1 1 | p1(t) | 1 0  
|
| p1(t) | 0 1 0 0 0 | p1(t) | 0 1  
|
| p1(t) | 0 0 0 0 0 | p1(t) | 0 1 1 1 |
Оскільки у першому випадку обставини, що вимагаються, досягаються за мінімальний час (один елементарний проміжок), то керування R (t) = 0 при t ≥ 0 є найкращим серед усіх можливих. Окрім того, воно зберігає найкращі обставини й в усі наступні моменти часу. Не виключено, розуміється, що у майбутньому поняття найкращих обставин може змінитися й доведеться змінювати керування.
Окрім експертних оцінок є ще й другий шлях установки залежностей s i(t) = F ij, який будемо називається ретроспективним аналізом. Припустимо, що відома історія зміни обстановки за достатньо тривалий проміжок часу. Якщо деяка формула s i(t) = f [ s i (t - t 1),…, s i
(t - t 1),…, s i (t - t p)] задовольнялася для переважної більшості моментів часу t = 0,-1,-2,...,- Т із заданого проміжку [– Т,0 ], то істотно припустити, що це буде мати місце й у найближчому майбутньому, і використати цю формулу поряд із залежностями, що задаються експертами.
(t - t p)] задовольнялася для переважної більшості моментів часу t = 0,-1,-2,...,- Т із заданого проміжку [– Т,0 ], то істотно припустити, що це буде мати місце й у найближчому майбутньому, і використати цю формулу поряд із залежностями, що задаються експертами.
Ретроспективний аналіз можна вживати також для уточнення ваг r ij експертних оцінок: ті оцінки, котрі мають багато підтверджень у минулому, збільшують свою вагу, та навпаки. Проте, далеко не завжди відсутність достатньо переконливих підтверджень експертної оцінки у ретроспективному плані може служити підставою для зменшення її значення у прогнозному плані. Не виключено, що експерт узяв до уваги фактори, що не увійшли у модель, та котрі не мали місця у минулому, проте будуть мати місце у майбутньому. Окрім того, хоча звичайно експертні оцінки залежать від порівняно невеликого числа параметрів, неявним чином кожний експерт враховує всю обстановку у цілому. А ця обстановка може бути суттєво іншою у майбутньому, ніж у минулому.
Техніка роботи із булевими моделями може бути поширена на довільні конечні моделі, тобто моделі з конечним числом параметрів, що приймають конечні множини значень (у загальному випадку різні для різних параметрів). Один із простіших (хоча й не самих економних) способів полягають ув наступному. Нехай, наприклад, конечний параметр приймає чотири різних значення: 2 (погано), 3 (задовільно), 4 (добре) та 5 (відмінно).
Параметр x може бути заміненим системою подій (булевих параметрів) s 1, s 2, s 3, s 4, що приймають значення 1 тоді, коли відповідно x = 2; x = 3; x = 4; x = 5. Залежності установлюються не для параметра x, а для подій s 1, s 2, s 3, s 4, що його замінюють. Істотною відміною від випадку звичайної булевої моделі є необхідність нормування отриманих ймовірностей. В якості справжніх значень ймовірностей p ΄i появи подій s i приймаються не імовірності p i, обчислені по формулам (**), а величини
p ΄i =  , (i =
, (i =  ).
).
У цьому випадку сума  дорівнює 1, як і повинно бути для ймовірностей повної системи незалежних подій.
дорівнює 1, як і повинно бути для ймовірностей повної системи незалежних подій.
Окрім розглянутого метода отримання об’єктивного знання про майбутній стан соціально-економічної системи існує ціла група потужних методів, як-то метод часових рядів, метод регресивного аналізу, як одномірного, так й множинного, імітаційне моделювання, економетричні моделі тощо. Усі вони відносяться до класу так званих методів кількісного прогнозування й застосовуються для наближеного „визначення” майбутньої поведінки деякої змінної величини або системи взаємозв’язаних змінних величин на зараннє відомому інтервалі часу.
Не дивлячись на широке практичне застосування цих методів та наявність значних обчислювальних потужностей, їх практичне використання принципово обмежується лише випадками опрацювання ретроспективних даних кількісного характеру про процеси, що монотонно змінюються. Інакше кажучи, при застосуванні методів прогнозування відбувається опис майбутнього, що фактично є продовженням або екстраполяцією минулого. Це суттєво обмежує можливості цих методів. Перш за усе тому, що ми живемо у світі, де постійно відбуваються якісно нові, не притаманні минулому, зміни. До них перш за усе відносяться різні стрибкоподібні зміни, що зв’язані із розривами монотонності процесів та мають характер суттєво нелінійних явищ.
Наприклад, на грані ХХ та ХХІ століть такими явищами були розпад Радянського Союзу, наступна за ним зміна геополітичної рівноваги у світі та ряд інших глобальних змін. За допомогою методів кількісного прогнозування подібні явища передбачити та організовано підготуватися до них не вдалося. Популярне у минулі 60-ті роки прогнозування з плином часу почало губити значення універсальної методології. Це зв’язано, перш за усе, із тим, що її методами не вдалося завбачити світову нафтову кризу початку 70-х років з її руйнівними наслідками, вибухоподібний розвиток інформаційних технологій у 90-х роках, фінансова криза у Південно-Східній Азії та у РФ 1998 року та багато інших глобальних змін.
Тому у сучасних умовах для системного аналітика усе більш актуальною стає нова задача – вміти передбачати майбутню поведінку або стан великої системи, які не можна інтерпретувати як звичайне продовження минулого, тому що це майбутнє може набути принципово відмінні форми та структури, порівняно із тим, що було відомо у минулому.
Відмічена проблема отримала назву передбачення, що як самостійна науково-практична методологія відбулася на початку 90-х років минулого століття.
Слід відмітити, що універсальних та досконалих підходів до розв’язку цієї проблеми до теперішнього часу не існує. Існують лише спроби побудови можливих сценаріїв тих чи інших явищ у майбутньому. Проте принциповою відмінністю від попередньої практики розв’язку подібних задач є те, що методи, які використовуються для цього, мають не кількісний, а якісний характер. Окремі з них були вже відомі досить давно. Наприклад, ще у 60-ті роки ХХ-го століття в американській компанії Rand Corporation розробили метод, що дозволив полегшати візуалізацію сценаріїв розроблення та застосування нової техніки в усіх технологічних аспектах. Цей метод отримав назву дельфійського.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 397; Нарушение авторских прав?; Мы поможем в написании вашей работы!