
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Визначення напрямку головних осей
|
|
|
|
Головні центральні моменти інерції і формули для їх визначення.
В інженерній практиці розрахунків важливе значення займають головні центральні осі, відцентровий момент інерції відносно яких дорівнює нулеві. Позначають такі осі буквами (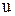 ) і (
) і (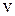 ). Таким чином:
). Таким чином:
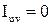 , а відповідно, Sy=Sz=0
, а відповідно, Sy=Sz=0
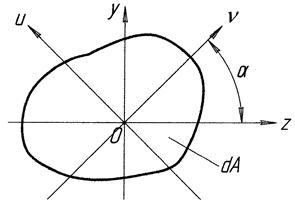 Візьмемо довільне тіло з прямокутною системою координат, що проходить через центр ваги тіла, повернемо його на деякий довільний кут
Візьмемо довільне тіло з прямокутною системою координат, що проходить через центр ваги тіла, повернемо його на деякий довільний кут 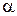 при якому відцентровий момент інерції буде рівний нулеві.
при якому відцентровий момент інерції буде рівний нулеві.
Позначимо осі цієї системи координат через (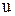 ) і (
) і (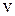 ).
).
Необхідно відмітити, що серед нескінченої множини центральних осей існує хоча б одна пара головних центральних осей.
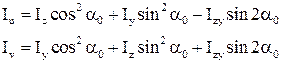 (1)
(1)
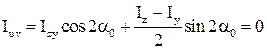 Þ
Þ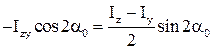
Розділимо цей вираз на 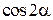 Þ
Þ
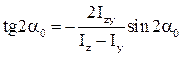 (2)
(2)
Із формули (2) визначаємо положення головних центральних осей інерції.
Слід нагадати, що додатні кути повороту осей відкладаються проти годинникової стрілки.
Використовуючи формули (1) запишемо вираз для суми і різниці головних центральних моментів інерції:
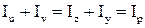 Þ
Þ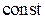 (3)
(3)
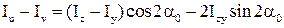 (4)
(4)
Використовуючи відношення (2) рівняння (4) запишемо в такому вигляді:
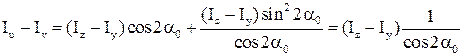
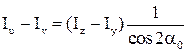
Оскільки: 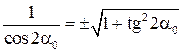 , то ми можемо записати:
, то ми можемо записати:  і підставимо цей вираз в формулу (2)–будемо мати:
і підставимо цей вираз в формулу (2)–будемо мати:
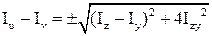
Додаючи і віднімаючи вирази (3) і (4) будемо мати:
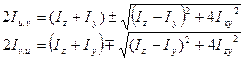
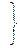 Þ
Þ

I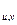
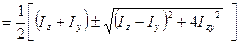 (5)
(5)
Iv,u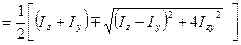
Причому верхні знаки необхідно брати при 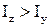 , а нижні – при
, а нижні – при 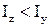 .
.
Таким чином формули (2) і (5) дозволяють визначити напрямок головних осей і величину головних центральних моментів інерції площі перерізу.
Головним центральним моментом інерції притаманна властивість екстремальності, тобто відносно головних осей інерції вони будуть мати максимальне значення.
Площина, що проведена через вісь стержня і його головні осі інерції носить назву головної площини перерізу.
6. Поняття про радіус інерції.
Любий момент інерції відносно осі можливо виразити, як добуток площі перерізу фігури на квадрат деякої відстані до цієї вісі.
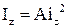
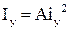 , де
, де 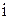 –радіус інерції
–радіус інерції
Звідси: 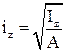 ; одиниці виміру
; одиниці виміру 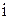 =(см)
=(см)
Відносно головних центральних осей:
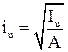

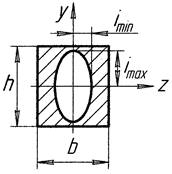 Приклади:
Приклади:
№1
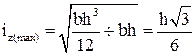 (см)
(см)
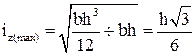 (см)
(см)
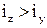 т.як
т.як 
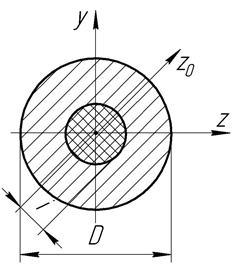
№2
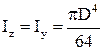

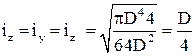
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 735; Нарушение авторских прав?; Мы поможем в написании вашей работы!