Лекція 6

Тема: Довжина і її вимірювання. Дії над відрізками. Властивості числових значень довжини.

Площа геометричних фігур і її вимірювання.

фізико-математичних дисциплін

_____________ Н.В.Назаренко

м. Берислав,

2009 р.

Тема лекції: Довжина і її вимірювання. Дії над відрізками. Властивості числових значень довжини. Площа геометричних фігур і її вимірювання.

Знати:

- поняття довжини відрізка і її вимірювання;

- властивості числових значень величини;

- стандартні одиниці довжини, відомості про їх походження;

- поняття площі многокутника, властивості площі;

- вимірювання площі фігури за допомогою палетки.

Вміти:

- будувати і вимірювати довжини відрізків за допомогою лінійки,

- порівнювати відрізки за допомогою вимірювання;

- обчислювати площу прямокутника, квадрата за довжинами їх сторін та інших фігур за допомогою палетки.

Тип лекції: тематична

Ключові поняття: довжина відрізка, вимірювання довжини відрізка, площа фігури, палетка.

План

1. Довжина відрізка і її вимірювання.

2. Дії над відрізками, їх властивості.

3. Многокутник і його елементи.

4. Площа фігури, властивості та її вимірювання.

5. Вимірювання площі фігури за допомогою палетки.

Основна література

1. Кухар В.М., Білий Б.М. Теоретичні основи початкового курсу математики: Навч. посібник для педучилищ. – К.: Вища школа, 1987. – 319 c.

2. Стойлова Л.П., Пишкало А.М. Основы начального курса математики: Учеб. пособие для учащихся педучилищ. – М.: Просвещение, 1988. – 320 c.

Структура лекції

1. Вступна частина:

Оголошення теми, мети і завдань лекції.

Ознайомлення з планом лекції, основною та додатковою літературою.

2. Виклад лекційного матеріалу (згідно плану та вимог до лекції).

І. Довжина відрізка і її вимірювання.

Означення. Довжиною відрізка називається додатня величина, визначена для кожного відрізка так, що:

1. Рівні відрізки мають рівні довжини;

2. Якщо відрізок складається із скінченого числа відрізків, то його довжина дорівнює сумі довжин цих відрізків.

Вимирювання довжини відрізка

Із множини відрізків вибирають який небудь відрізок е і беруть його за одиницю довжини. На відрізку а від одного з його кінця відкладають послідовно відрізки, рівні е, до тих пір, поки це можливо. Якщо відрізки, рівні е, відклались n разів і кінець останнього співпав з кінцем відрізка а, то кажуть, що значення довжини відрізка а є натуральне число n і пишуть: а = n · е. якщо е – частина відрізка а, що не вимірюється відрізком е, тоді 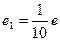, то 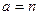, і значення довжини відрізка а є скінчений десятинний дріб. Якщо ж відрізок 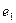відклався раз і залишилася ще частина, менша 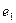, то на ньому відкладають відрізки, рівні , то , .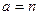

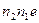Може бути значення довжини відрізка а – нескінченний десятковий дріб, тобто довжина відрізка може бути представлена додатнім дійсним числом і навпаки.

ІІ. Дії над відрізками, їх властивості.

Властивості довжини відрізка

1. При вибраній одиниці довжини, довжина будь-якого відрізка виражається додатнім дійсним числом і для кожного додатнього дійсного числа є відрізок, довжина якого виражається цілим числом.

2. Якщо два відрізки рівні, то числові значення їх довжин також рівні і навпаки.

3. Якщо даний відрізок є сума декількох відрізків, то числове значення його довжини дорівнює сумі числових значень довжин відрізків доданків і навпаки.

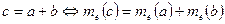
4. Якщо довжини відрізків а і b такі, що b = х · а, де х – додатнє дійсне число і довжина а виміряна за допомогою одиничного відрізка е, то, щоб знайти числове значення відрізку b при одиничному відрізку е, достатньо число х помножити на числове значення довжини а при одиничному відрізку е.

5. При заміні одиниці довжини числове значення довжини збільшується (зменшується) в стільки ж разів, в скільки нова одиниця менша (більша) «старої».

5 км = 5000 м

25 м = 0,025 км

6. Якщо відрізок а > b, то його числове значення більше числового значення відрізка b при одній і тій же одиниці довжини.

а > b >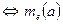

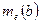
7. Якщо відрізок с – є різницею відрізків а і b, то його числове значення дорівнює різниці числових значень цих відрізків при одній і тій же одиниці вимірювання.

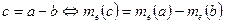
8. Щоб знайти відношення відрізків, треба знайти відношення числових значень довжини цих відрізків при заданій одній і тій же одиниці вимірювання е.

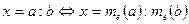
ІІІ. Многокутник і його елементи.

Означення. Многокутник – це замкнена ламана лінія.

Якщо замкнена лінія розглядається на площині, то можна говорити про площу многокутника.

Многокутник має: вершини, сторони і кути. По кількості кутів і сторін, многокутник має назву.

B

A П’ятикутник

F C

D

ІV. Площа фігури, властивості та її вимірювання.

Означення. Площею фігури називається невід’ємна величина, визначена для кожної фігури так, що:

1) рівні фігури мають рівні площі;

2) якщо фігура складена із скінченого числа фігур, то її площа рівна сумі площ цих фігур.

S(F) - площа е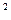– площа одиничного квадрата.

S(F) = х · е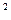, х – числове значення площі.

S(F) = 35 м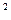(площа класної кімнати)

Властивості площі:

1. Якщо фігури рівні, то рівні числові значення їх площ (одна і та ж одиниця площі). Фігури, у яких площі рівні, називаються рівновеликими.

2. Якщо F складена із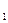 FF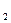,... F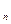, то числове значення площі Fдорівнює сумі числових значень площ цих фігур (при одній і тій же одиниці площі).

3. При заміні одиниці площі числове значення збільшується (зменшується) у стільки раз, в скільки нова одиниця менша (більша) «старої».

1 см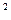= 0,01 дм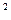(у 100 разів).

V. Вимірювання площі фігури за допомогою палетки.

Означення. Палетка – це прозора плівка з нанесеними на неї квадратними сантиметрами.

За допомогою неї вимірюють площі фігур, що не мають форми геометричного тіла.

m – кількість квадратів, які лежать всередині фігури.

n – число квадратів через які проходять контури фігури.

< S(F) <

S(F), отже

S(F) =

Таблиця мір площі

1 мм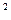– площа квадрата, сторона якого 1 мм.

1 см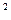– площа квадрата, сторона якого 1 см.

1 дм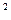– площа квадрата, сторона якого 1 дм.

1 м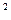– площа квадрата, сторона якого 1 м.

Ар (а) – площа квадрата, сторона якого 10 м (сотка).

Гектар (га) – площа квадрата, сторона якого 100 м.

1 км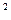– площа квадрата, сторона якого 1 км.

1 га = 10 000 м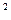

1 а = 100 м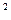

1 м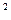= 100 дм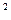

1 м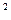= 10 000 см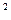

1 см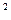= 100 мм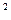

3. Заключна частина:

Загальний висновок.

Відповіді на запитання студентів.

Д/з: Стойлова Л.П., Пишкало А.М. Основы начального курса математики, § 18, п. 108 – 109, впр.1, 3, 4, 8, (С.291), 7, 8 (С.296)