Силовий розрахунок закатувальної машини

Якщо не враховувати силу тертя, то можна сказати, що лінія дії притискаючого зусилля Р проходить через вісь обертання ролика, а також через точку В, яка ділить дугу захоплення а-а навпіл (Рис.24.9).

Розкладемо силу Р на нормальну N і дотичну Т до окружності патрона, одержимо N = P×cosa; T = P×sina.

При обертанні під дією нормальної сили N виникає сила тертя F, яка також діє по дотичній до патрона, але направлена в сторону, протилежну Т.

Очевидно, що закатування можливе тільки в тому випадку, коли сила тертя F ³ T.

Оскільки F = f ×N, то P×sina £ f × P×cosa або tg a £ f, де f - коефіцієнт тертя.

Момент закатування М = Р×а, найбільше значення якого буде при tga = f. Плече

a = r_a×sina.

Рис.24.9. Схема сил, що діють на патрон в процесі закатування банки

Оскільки

,

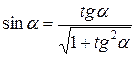то

При закатуванні роликом першої операції осьове зусилля стиснення повинно запобігти провертання корпусу відносно кришки. Перевищення допустимого стиснення може привести до пошкодження ущільнюючої плівки або деформації фланця.

В даному випадку допустиме значення осьового стиснення рівне

де F – контактна поверхня фланця;

q - допустимий тиск для каучукової плівки не більше 3,0 Мн/м² (30кГ/см²).

При другій операції закатування роликом, а саме загинання місця потовщення (переріз повздовжнього і закатувального шва) приводить до різкого збільшення дотичної складової Т, оскільки кут a збільшується. Тому амортизаційну пружину повзуна розраховують з умови, що момент тертя від стиснення банки в патронах рівний моменту закатування, а необхідне зусилля встановлюється ступенем стиснення пружини.

Осьове навантаження сприймається коловою площадкою закатувального патрона (Рис.24.10), для якого момент тертя

,

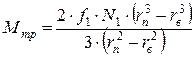де f_{1 -} коефіцієнт тертя;

N₁ - осьове зусилля стискання;

r_n - радіус патрона (нижній);

r_в - радіус виточки.

Рис.24.10. Схема дії сил в процесі стискання банки

Прирівнюючи значення М_тр і М, отримаємо

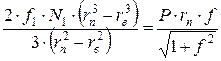
і

.

Враховуючи специфічні умови роботи деталей, для розрахунків слід приймати f₁ - 0,09 - 0,1, а для f - 0,14-0,15. Крім того, для уникнення можливих проковзувань банки в патронах в початковий момент, дійсну величину осьового зусилля N_д слід збільшити на величину коефіцієнта запасу k = 1,1 -1,2

N_д = k N

В випадку примусового обертання не тільки верхнього, але і нижнього патрона величина моменту тертя

,

а зусилля стискання N₁ відповідно зменшується.

Для бляхи товщиною до 0,3 мм при діаметрі банки до 100 мм притискне зусилля Р приблизно рівне 1600 - 1800 н. Основні розміри амортизаційної пружини визначаються з рівняння

,

де G - модуль пружності при зсуві;

D - середній діаметр витка пружини, в даному випадку рівний 34 мм;

d - діаметр дроту (рівний 6 мм);

l - усадка витків пружини;

n - число робочих витків (рівне 4).

Дата добавления: 2014-01-07