Закон Джоуля – Ленца

З проходженням струму через провідник, який має опір, нерозривно зв'язане виділення теплоти. Визначимо кількість теплоти, що виділяється за одиницю часу на визначеній ділянці кола. Нехай однорідна ділянка знаходиться між перетинами 1 і 2 провідника. Знайдемо роботу, яку виконують сили поля над носіями струму на ділянці 1-2 за час dt.

Якщо сила струму в провіднику дорівнює І, то за час dt через кожен перетин провідника пройде заряд dq = Іdt. Тому чинена при такому переносі робота сил поля:

.

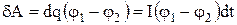Відповідно до закону збереження енергії еквівалентна цій роботі енергія повинна виділятися в іншій формі. Якщо провідник нерухомий і в ньому не відбуваються хімічні перетворення, то ця енергія повинна виділятися у формі внутрішньої (теплової) енергії, у результаті чого провідник нагрівається, при цьому теплота, що виділяється в провіднику дорівнює роботі струму:

.

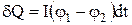А оскільки за законом Ома , то в остаточному підсумку одержуємо:

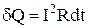
Ця формула виражає закон Джоуля-Ленца: Кількість теплоти, що виділяється в провіднику при протіканні по ньому струму прямо пропорційно квадрату сили струму, опору провідника і часу протікання струму.

Одержимо вираження цього закону в локальній формі, що характеризує виділення теплоти в різних місцях провідного середовища. Для цієї мети виділимо в даному середовищі елементарний об’єм у вигляді циліндрика з утворюючими, рівнобіжними вектора густини струму в даному місці. Нехай поперечний переріз циліндрика dS, а його довжина dl. Тоді на підставі закону Джоуля–Ленца в цьому об’ємі за час dt виділяється кількість теплоти:

,

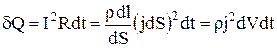де dV = dSdl – об’єм циліндрика. Розділивши останнє рівняння на dVdt, одержимо формулу, що визначає кількість теплоти, що виділяється за одиницю часу в одиниці об'єму провідного середовища – питому теплову потужність струму:

.

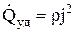Ця формула виражає закон Джоуля-Ленца в локальній формі: питома теплова потужність струму пропорційна квадрату густини електричного струму і питомому опору середовища в даній точці.

Якщо на носії струму діють тільки електричні сили, то на підставі закону Ома локальний закон Джоуля-Ленца приймає вигляд:

.

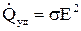Якщо ділянка кола неоднорідна, тобто містить джерело ЕРС, то на носії струму будуть діяти не тільки електричні сили, але і сторонні. У цьому випадку виділюване в нерухомому провіднику тепло буде дорівнює за законом збереження енергії алгебраїчній сумі робіт електричних і сторонніх сил. Це ж відноситься і до відповідних потужностей: теплова потужність повинна бути рівною алгебраїчній сумі потужностей електричних і сторонніх сил.

За законом Ома для неоднорідної ділянки кола: 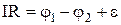. Помножимо ліву і праву частини останньої рівності на силу струму І:

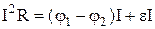
Тут ліворуч стоїть теплова потужність, що виділяється на ділянці 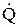. При наявності сторонніх сил величина 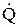визначається формулою:

.

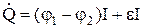Останній доданок праворуч являє собою потужність, що розвивається сторонніми силами на даній ділянці.

Таким чином, отримане рівняння означає, що теплова потужність, що виділяється на ділянці кола між точками 1 і 2, дорівнює алгебраїчній сумі потужностей електричних і сторонніх сил. Суму цих потужностей називають потужністю струму на розглянутій ділянці кола. У випадку нерухомої ділянки кола потужність виділюваної на цій ділянці теплоти дорівнює потужності струму. Для замкнутого нерозгалуженого кола j₁ = j₂ і питома теплова потужність дорівнює:

,

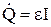тобто, загальна кількість виділюваної за одиницю часу у всьому колі джоулевої теплоти дорівнює потужності тільки сторонніх сил. Виходить, що теплота виробляється тільки сторонніми силами. Роль же електричного поля зводиться до того, що воно перерозподіляє цю теплоту по різних ділянках кола.

Дата добавления: 2014-01-07