
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема: Речовина у магнітному полі. Магнетики. Напруженість магнітного поля. Теорема про циркуляцію вектора напруженості
|
|
|
|
Лекція №28
Якщо в магнітне поле ввести речовину, поле зміниться. Це пояснюється тим, що всяка речовина є магнетиком, тобто вона здатна під дією магнітного поля намагнічуватися – здобувати магнітний момент. Намагнічена речовина створює своє магнітне поле  , яке разом з первинним полем
, яке разом з первинним полем  утворює результуюче поле з індукцією:
утворює результуюче поле з індукцією: 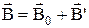 . Тут під
. Тут під  і
і  маються на увазі поля, що усереднені по фізично нескінченно малому об’єму. Поля
маються на увазі поля, що усереднені по фізично нескінченно малому об’єму. Поля  і
і  не мають джерел (магнітних зарядів), тому для результуючого поля
не мають джерел (магнітних зарядів), тому для результуючого поля 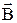 при наявності магнетика справедлива теорема Гауса:
при наявності магнетика справедлива теорема Гауса: 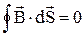 . Це означає, що лінії вектора
. Це означає, що лінії вектора 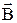 і при наявності речовини залишаються усюди безперервними.
і при наявності речовини залишаються усюди безперервними.
Механізм намагнічування. В даний час установлено, що молекули багатьох речовин мають власний магнітним момент, який обумовлений внутрішнім рухом зарядів. Кожному магнітному моментові відповідає елементарний круговий струм, що створює в навколишньому просторі магнітне поле. При відсутності зовнішнього магнітного поля магнітні моменти молекул орієнтовані безпорядково, тому обумовлене ними результуюче магнітне поле дорівнює нулю.
Якщо ж речовину помістити в зовнішнє магнітне поле, то під дією цього поля магнітні моменти молекул орієнтуються переважно в одному напрямку, і речовина намагнічується, тобто його сумарний магнітний момент стає відмінним від нуля. При цьому магнітні поля окремих молекул вже не компенсують один одного, у результаті чого виникає поле .
.
Інакше відбувається намагнічування речовин, молекули яких при відсутності зовнішнього поля не мають магнітного моменту. Внесення таких речовин у зовнішнє поле індуцирує елементарні кругові струми в молекулах, і молекули, а разом з ними і уся речовина здобувають магнітний момент, що також приводить до виникнення поля . Більшість речовин при внесенні в магнітне поле намагнічуються слабко. Сильними магнітними властивостями володіють тільки феромагнітні речовини: залізо, нікель, кобальт, багато їхніх сплавів і ін.
. Більшість речовин при внесенні в магнітне поле намагнічуються слабко. Сильними магнітними властивостями володіють тільки феромагнітні речовини: залізо, нікель, кобальт, багато їхніх сплавів і ін.
 Намагніченість. Ступінь намагнічування магнетика характеризують магнітним моментом одиниці об'єму. Цю величину називають намагніченістю і позначають
Намагніченість. Ступінь намагнічування магнетика характеризують магнітним моментом одиниці об'єму. Цю величину називають намагніченістю і позначають 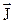 . По визначенню:
. По визначенню: 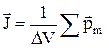 , де DV - фізично нескінченно малий об’єм в околиці даної точки,
, де DV - фізично нескінченно малий об’єм в околиці даної точки, 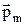 – магнітний момент окремої молекули. Якщо у магнетику N молекул, то можна записати:
– магнітний момент окремої молекули. Якщо у магнетику N молекул, то можна записати:  , де n – концентрація молекул,
, де n – концентрація молекул,  – середній магнітний момент однієї молекули. Намагнічування речовини обумовлено переважною орієнтацією магнітних моментів окремих молекул в одному напрямку. Це ж можна сказати і про елементарні кругові струми, що зв'язані з кожною молекулою. Їх називають молекулярними струмами. Така поведінка молекулярних струмів приводить до появи макроскопічних струмів
– середній магнітний момент однієї молекули. Намагнічування речовини обумовлено переважною орієнтацією магнітних моментів окремих молекул в одному напрямку. Це ж можна сказати і про елементарні кругові струми, що зв'язані з кожною молекулою. Їх називають молекулярними струмами. Така поведінка молекулярних струмів приводить до появи макроскопічних струмів 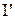 , які називають струмами намагнічування. Звичайні струми, що течуть по провідниках і зв'язані з переміщенням у речовині носіїв струму, називають струмами провідності І. Розглянемо циліндр із однорідного магнетика, намагніченість якого однорідна і спрямована вздовж вісі. Виникнення струмів намагнічування пояснюється тим, що у сусідніх молекул намагніченої речовини молекулярні струми в місцях їхнього зіткнення течуть у протилежних напрямках і взаємно компенсують один одного. Некомпенсованими залишаються тільки ті молекулярні струми, що виходять на бічну поверхню циліндра. Ці струми і утворять макроскопічний поверхневий струм намагнічування I’, що циркулює по бічній поверхні циліндра. Струм I’ збуджує таке ж макроскопічне магнітне поле, що і взяті разом молекулярні струми.
, які називають струмами намагнічування. Звичайні струми, що течуть по провідниках і зв'язані з переміщенням у речовині носіїв струму, називають струмами провідності І. Розглянемо циліндр із однорідного магнетика, намагніченість якого однорідна і спрямована вздовж вісі. Виникнення струмів намагнічування пояснюється тим, що у сусідніх молекул намагніченої речовини молекулярні струми в місцях їхнього зіткнення течуть у протилежних напрямках і взаємно компенсують один одного. Некомпенсованими залишаються тільки ті молекулярні струми, що виходять на бічну поверхню циліндра. Ці струми і утворять макроскопічний поверхневий струм намагнічування I’, що циркулює по бічній поверхні циліндра. Струм I’ збуджує таке ж макроскопічне магнітне поле, що і взяті разом молекулярні струми.
Теорема про циркуляцію вектора намагнічування. Циркуляція вектора намагнічування по довільному замкненому контуру дорівнює алгебраїчній сумі струмів намагнічування, що охоплює цей контур:  , де
, де 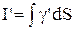 і інтегрування виконується по довільній поверхні, що натягнута на виділений контур.
і інтегрування виконується по довільній поверхні, що натягнута на виділений контур.
Вектор напруженості магнітного поля. Теорема про циркуляцію вектора напруженості. У магнетиках, які знаходяться у зовнішньому магнітному полі, виникають струми намагнічування, тому циркуляція вектора 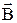 визначається не тільки струмами провідності, але і струмами намагнічування:
визначається не тільки струмами провідності, але і струмами намагнічування: 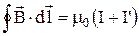 , де I і
, де I і 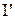 – струми провідності і намагнічування, охоплюваних заданим контуром. Через те, що визначення струмів намагнічування
– струми провідності і намагнічування, охоплюваних заданим контуром. Через те, що визначення струмів намагнічування 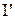 у загальному випадку задача досить складна, використаємо математичний вираз теореми про циркуляцію вектора намагнічування
у загальному випадку задача досить складна, використаємо математичний вираз теореми про циркуляцію вектора намагнічування  , підставивши її в останню формулу. У підсумку отримаємо:
, підставивши її в останню формулу. У підсумку отримаємо: 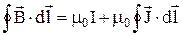 ,
,  . Величину, що стоїть під інтегралом у дужках, позначають буквою Н і називають напруженістю магнітного поля:
. Величину, що стоїть під інтегралом у дужках, позначають буквою Н і називають напруженістю магнітного поля: 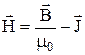 . Враховуючи поняття напруженості, отримуємо формулу, яка є математичним виразом теореми про циркуляцію вектора напруженості:
. Враховуючи поняття напруженості, отримуємо формулу, яка є математичним виразом теореми про циркуляцію вектора напруженості:  .
.
- Циркуляція вектора напруженості по довільному замкнутому контуру дорівнює алгебраїчній сумі струмів провідності, що охоплюються цим контуром.
Правило знаків для струмів те ж, що й у випадку циркуляції вектора магнітної індукції 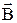 . Із отриманої формули випливає, що одиниці напруженості в СІ [А/м]. В диференційній формі теорема про циркуляцію вектора напруженості має вигляд:
. Із отриманої формули випливає, що одиниці напруженості в СІ [А/м]. В диференційній формі теорема про циркуляцію вектора напруженості має вигляд: 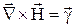 , тобто ротор вектора напруженості магнітного поля дорівнює густині струму провідності у тій же точці речовини.
, тобто ротор вектора напруженості магнітного поля дорівнює густині струму провідності у тій же точці речовини.
Зв'язок між векторами густини струму провідності і напруженістю магнітного поля. Відомо, що намагніченість 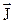 залежить від магнітної індукції
залежить від магнітної індукції 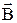 в даній точці речовини. Однак намагніченість прийнято зв'язувати не з магнітною індукцією, а з напруженість магнітного поля. Для деяких магнетиків залежність між векторами
в даній точці речовини. Однак намагніченість прийнято зв'язувати не з магнітною індукцією, а з напруженість магнітного поля. Для деяких магнетиків залежність між векторами 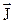 і
і  має лінійний характер, а саме:
має лінійний характер, а саме:  , де коефіцієнт c – магнітна сприйнятливість, безрозмірна величина, характерна для кожного даного магнетика. На відміну від діелектричної сприйнятливості c, яка завжди позитивна, магнітна сприйнятливість буває як позитивною, так і негативною. Відповідно магнетики, що підкоряються отриманій залежності, підрозділяють на парамагнетики (c > 0) і діамагнетики (c < 0). У парамагнетиків
, де коефіцієнт c – магнітна сприйнятливість, безрозмірна величина, характерна для кожного даного магнетика. На відміну від діелектричної сприйнятливості c, яка завжди позитивна, магнітна сприйнятливість буває як позитивною, так і негативною. Відповідно магнетики, що підкоряються отриманій залежності, підрозділяють на парамагнетики (c > 0) і діамагнетики (c < 0). У парамагнетиків 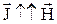 , у діамагнетиків
, у діамагнетиків  . Слід відзначити, що крім цих магнетиків існують феромагнетики, у яких залежність J(H) має досить складний характер: вона не лінійна і, крім того, спостерігається гістерезис, тобто залежність намагнічування від передісторії магнетика. Отримаємо зв’язок між векторами магнітної індукції і напруженості магнітного поля. Так як
. Слід відзначити, що крім цих магнетиків існують феромагнетики, у яких залежність J(H) має досить складний характер: вона не лінійна і, крім того, спостерігається гістерезис, тобто залежність намагнічування від передісторії магнетика. Отримаємо зв’язок між векторами магнітної індукції і напруженості магнітного поля. Так як 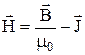 і
і  , після відповідної заміни маємо:
, після відповідної заміни маємо: 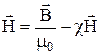 , відкіля отримаємо:
, відкіля отримаємо: 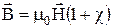 . Якщо ввести заміну
. Якщо ввести заміну  , то остання формула приймає вигляд:
, то остання формула приймає вигляд: 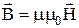 . Коефіцієнт m називають магнітною проникністю речовини. У парамагнетиків m > 1, у діамагнетиків m < 1, причому як у тих, так і в інших m відрізняється від одиниці досить мало, тобто магнітні властивості цих магнетиків виражені дуже слабко.
. Коефіцієнт m називають магнітною проникністю речовини. У парамагнетиків m > 1, у діамагнетиків m < 1, причому як у тих, так і в інших m відрізняється від одиниці досить мало, тобто магнітні властивості цих магнетиків виражені дуже слабко.
 Граничні умови для векторів
Граничні умови для векторів 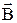 і
і  . Для векторів
. Для векторів 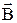 і
і  теорема Гауса має вигляд:
теорема Гауса має вигляд: 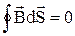 і
і  . Розглянемо нормальні складові векторів
. Розглянемо нормальні складові векторів 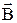 і
і  . Нехай циліндрик маленької висоти розташований на межі розділу двох магнетиків. Тоді теорема Гауса для вектора
. Нехай циліндрик маленької висоти розташований на межі розділу двох магнетиків. Тоді теорема Гауса для вектора 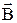 в проекціях на загальну нормаль
в проекціях на загальну нормаль 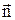 має вигляд:
має вигляд:  , відкіля отримуємо:
, відкіля отримуємо:  . Оскільки
. Оскільки  і
і 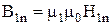 , то після відповідної заміни отримуємо:
, то після відповідної заміни отримуємо:  .
.
Висновок: Нормальна складова вектора 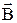 на межі розділу магнетиків не заломлюється, а нормальна складова вектора напруженості зазнає заломлення.
на межі розділу магнетиків не заломлюється, а нормальна складова вектора напруженості зазнає заломлення.
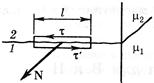 Розглянемо тангенціальну складову ліній
Розглянемо тангенціальну складову ліній 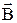 і
і  на межі розділу двох магнетиків. Використаємо теорему про циркуляцію вектора напруженості для малого прямокутного контуру, висота якого зневажливо мала по відношенню до його довжини l. Оскільки струмів проводи мості на межі розділу немає, то
на межі розділу двох магнетиків. Використаємо теорему про циркуляцію вектора напруженості для малого прямокутного контуру, висота якого зневажливо мала по відношенню до його довжини l. Оскільки струмів проводи мості на межі розділу немає, то  , відкіля випливає:
, відкіля випливає: 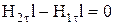 і
і  . Використовуючи зв’язок між векторами
. Використовуючи зв’язок між векторами 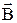 і
і  , отримуємо:
, отримуємо: 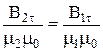 і
і 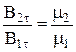 .
.
Висновок: Тангенціальна складова вектора напруженості на межі розділу магнетиків не заломлюється, а тангенціальна складова вектора магнітної індукції зазнає заломлення.
Феромагнетики і їхні властивості. Петля гістерезису.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2775; Нарушение авторских прав?; Мы поможем в написании вашей работы!