
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрична оптика
|
|
|
|
Тема: Історичний огляд вчення про світло. Світові хвилі і їхні характеристики. Електромагнітна хвиля на межі розділу. Показник заломлення. Принцип Ферма. Закони геометричної оптики.
Лекція № 36.
У кінці XVII століття на основі багатовікового досвіду і розвитку представлень про світло виникли дві теорії світла: корпускулярна (І. Ньютон) і хвильова (Р. Гук і X. Гюйгенс).
Відповідно до корпускулярної теорії, світло являє собою потік частинок (корпускул), що випускаються світними тілами і летять по прямолінійних траєкторіях. Рух світлових корпускул Ньютон підкорив сформульованим їм законам механіки. Відповідно до хвильової теорії, світло являє собою пружну хвилю, що поширюється в особливому середовищі – ефірі. Ефір заповнює весь світовий простір, пронизує всі тіла і має механічні властивості – пружність і густину. Згідно Гюйгенса, велика швидкість поширення світла обумовлена особливими властивостями ефіру. На сучасному етапі прийнята подвійна корпускулярно–хвильова теорія світла, у відповідності з якою світло являє собою єдність протилежних видів рухів – корпускулярного (квантового) та хвильового (електромагнітного).
Показник заломлення. Електромагнітна хвиля характеризується векторами 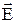 і
і 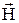 . Оскільки практично всі дії світла зв'язані з вектором
. Оскільки практично всі дії світла зв'язані з вектором 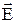 , прийнято говорити про світловий вектор, маючи на увазі вектор
, прийнято говорити про світловий вектор, маючи на увазі вектор 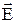 . Показник заломлення n деякого середовища визначають як
. Показник заломлення n деякого середовища визначають як 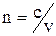 , де с – швидкість світла у вакуумі, v – фазова швидкість у даному середовищі. Оскільки
, де с – швидкість світла у вакуумі, v – фазова швидкість у даному середовищі. Оскільки 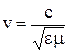 , а в немагнітному середовищі
, а в немагнітному середовищі 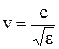 , то формулу показника заломлення можна отримати у вигляді:
, то формулу показника заломлення можна отримати у вигляді: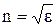 . Остання формула зв'язує оптичні властивості речовини з його електричними властивостями. Показник заломлення характеризує оптичну густину середовища. Середовище з великим показником заломлення називають оптично більш густою.
. Остання формула зв'язує оптичні властивості речовини з його електричними властивостями. Показник заломлення характеризує оптичну густину середовища. Середовище з великим показником заломлення називають оптично більш густою.
У речовині довжина хвилі 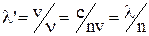 . Таким чином, при переході з вакууму у середовище довжина хвилі світла зменшується в n разів.
. Таким чином, при переході з вакууму у середовище довжина хвилі світла зменшується в n разів.
Інтенсивність хвилі. Світлову хвилю характеризують інтенсивністю І – це модуль середнього за часом значення густини потоку енергії. Густина потоку електромагнітної енергії визначається вектором Пойнтинга П як 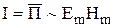 . Оскільки
. Оскільки 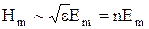 , то формулу інтенсивності світла можна представити так:
, то формулу інтенсивності світла можна представити так: 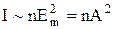 . Із отриманої формули свідчить, що інтенсивність світла прямо пропорційна амплітуді коливань електромагнітної хвилі.
. Із отриманої формули свідчить, що інтенсивність світла прямо пропорційна амплітуді коливань електромагнітної хвилі.
Електромагнітна хвиля на границі розділу. Нехай плоска електромагнітна хвиля падає нормально на границю розділу двох однорідних ізотропних прозорих діелектриків, магнітна проникність яких дорівнює одиниці, а показники заломлення 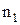 і
і 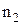 . Відомо, що при цьому виникають відбита і заломлена хвилі.
. Відомо, що при цьому виникають відбита і заломлена хвилі. 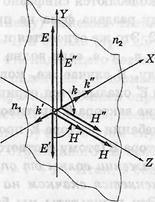
Позначимо електричну складову в падаючих, відбитих і переломленій хвилях відповідно через 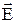 ,
, 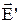 і
і  , а магнітну складову – через
, а магнітну складову – через 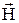 ,
, 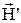 і
і 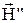 . З розумінь симетрії ясно, що коливання векторів
. З розумінь симетрії ясно, що коливання векторів 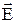 ,
, 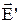 і
і  відбуваються в одній площині. Це ж відноситься і до векторів
відбуваються в одній площині. Це ж відноситься і до векторів 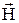 ,
, 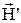 і
і 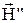 . Скористаємося граничними умовами для тангенціальних складових векторів
. Скористаємося граничними умовами для тангенціальних складових векторів 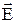 і
і 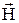 :
: 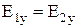 ,
, 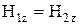 . Для розглядуваного випадку ці умови мають вигляд:
. Для розглядуваного випадку ці умови мають вигляд:  ,
, 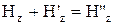 . Оскільки
. Оскільки 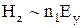 ,
, 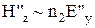 , і
, і 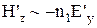 (проекції
(проекції 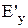 і
і 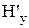 у відбитій хвилі мають протилежні знаки), то можна записати:
у відбитій хвилі мають протилежні знаки), то можна записати: 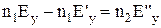 або
або 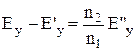 , Із отриманих виразів знайдемо
, Із отриманих виразів знайдемо 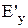 і
і 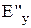 :
: 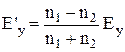 ;
; 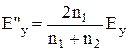 , або у векторному вигляді:
, або у векторному вигляді: 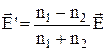 ;
; 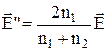 .
.
Звідси випливає, що:
- вектор  завжди співпадає за напрямом з вектором
завжди співпадає за напрямом з вектором 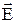 , тобто обидва вектори коливаються синфазно – при проходженні хвилі через границю розділу фаза не змінюється.
, тобто обидва вектори коливаються синфазно – при проходженні хвилі через границю розділу фаза не змінюється.
- за умови 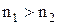 , тобто якщо хвиля переходить в оптично менш густе середовище, вектори
, тобто якщо хвиля переходить в оптично менш густе середовище, вектори 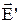 і
і 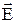 теж співпадають за напрямом.
теж співпадають за напрямом.
- якщо 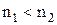 , тобто якщо хвиля переходить в оптично більш густіше середовище, вектори
, тобто якщо хвиля переходить в оптично більш густіше середовище, вектори 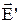 і
і 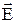 протилежно спрямовані. При цьому коливання вектора
протилежно спрямовані. При цьому коливання вектора 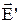 відбуваються в противофазі з коливаннями вектора
відбуваються в противофазі з коливаннями вектора 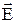 . Іншими словами, при відбиванні хвилі від оптично більш густого середовища її фаза змінюється стрибком на p.
. Іншими словами, при відбиванні хвилі від оптично більш густого середовища її фаза змінюється стрибком на p.
Довжини світлових хвиль, сприйманих оком, дуже малі (менш 1 мкм). Тому в багатьох випадках можна вважати, що світло являє собою потік світлових променів. В цьому випадку закони оптики можна сформулювати мовою геометрії. Відповідний розділ оптики називають геометричною оптикою.
Основу геометричної оптики складають три закони:
1. Закон прямолінійного поширення світла: в однорідному середовищі світло розповсюджується прямолінійно.
2. Закон відображення світла: Падаючий промінь, відображений промінь, і перпендикуляр до поверхні, проведений до точки падіння, лежать в одній площині. Кут відображення 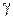 світла дорівнює його кутові падіння
світла дорівнює його кутові падіння 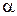 :
: 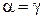 .
.
3. Закон заломлення світла (закон Снелла): при переломленні світла на границі розділу двох ізотропних середовищ з показниками заломлення 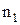 і
і 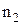 виконується умова:
виконується умова: 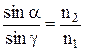 . При цьому падаючий промінь, заломлений промінь і нормаль до точки падіння лежать у одній площині. Звідси також випливає, що при падінні світла на оптично менш густе середовище (
. При цьому падаючий промінь, заломлений промінь і нормаль до точки падіння лежать у одній площині. Звідси також випливає, що при падінні світла на оптично менш густе середовище (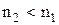 ) кут b може досягти 90°. Відповідний кут падіння називають граничним, а явище, при якому світло повність відображається від межі розділу середовищ, називається явищем повного внутрішнього відображення. Закон заломлення для граничного випадку повного внутрішнього відображення має вигляд:
) кут b може досягти 90°. Відповідний кут падіння називають граничним, а явище, при якому світло повність відображається від межі розділу середовищ, називається явищем повного внутрішнього відображення. Закон заломлення для граничного випадку повного внутрішнього відображення має вигляд: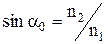 .
.
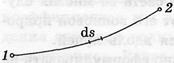 Принцип Ферма. Розглянемо шлях 1–2, що проходить промінь світла в неоднорідному середовищі. Ділянка шляху ds світло проходить за час dt = ds/v, де v – швидкість світла в даному місці. Так як
Принцип Ферма. Розглянемо шлях 1–2, що проходить промінь світла в неоднорідному середовищі. Ділянка шляху ds світло проходить за час dt = ds/v, де v – швидкість світла в даному місці. Так як 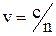 , то
, то 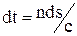 , і час t для проходження світлом шляху 1–2 дорівнює
, і час t для проходження світлом шляху 1–2 дорівнює 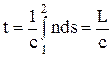 , де
, де  називають оптичною довжиною шляху. В однорідному середовищі
називають оптичною довжиною шляху. В однорідному середовищі 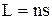 , де s – геометричний шлях. Слід відзначити, що оптична довжина шляху L еквівалентна за часом поширенню світла у вакуумі, тобто час поширення світла на шляху s у речовині зі швидкістю v такий самий, як у вакуумі зі швидкістю с на шляху L. Принцип Ферма стверджує: світло поширюється по такому шляху, оптична довжина якого мінімальна, тобто на проходження шляху світло повинно витратити мінімальний час.
, де s – геометричний шлях. Слід відзначити, що оптична довжина шляху L еквівалентна за часом поширенню світла у вакуумі, тобто час поширення світла на шляху s у речовині зі швидкістю v такий самий, як у вакуумі зі швидкістю с на шляху L. Принцип Ферма стверджує: світло поширюється по такому шляху, оптична довжина якого мінімальна, тобто на проходження шляху світло повинно витратити мінімальний час.
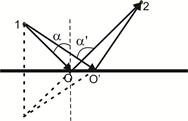 Отримаємо з принципу Ферма закони геометричної оптики. Нехай світло попадає з точки 1 у точку 2. Тут можливі відразу два випадки: прямій шлях 1-2 і при відображенні від границі роздягнула двох однорідних середовищ на шляху 102. Середовище, у якій поширюється промінь, однорідна, тому мінімальність оптичної довжини шляхи зводиться до мінімальності його геометричної довжини. З малюнку видно, що прямий шлях 1–2 дійсно мінімальний: найближчі до нього будуть довше. Те ж можна сказати і про шляху 102. Він виявляється теж мінімальним за умовою виконання закону відображення, тобто
Отримаємо з принципу Ферма закони геометричної оптики. Нехай світло попадає з точки 1 у точку 2. Тут можливі відразу два випадки: прямій шлях 1-2 і при відображенні від границі роздягнула двох однорідних середовищ на шляху 102. Середовище, у якій поширюється промінь, однорідна, тому мінімальність оптичної довжини шляхи зводиться до мінімальності його геометричної довжини. З малюнку видно, що прямий шлях 1–2 дійсно мінімальний: найближчі до нього будуть довше. Те ж можна сказати і про шляху 102. Він виявляється теж мінімальним за умовою виконання закону відображення, тобто 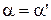 . Одержимо за допомогою принципу Ферма закон заломлення світла на границі розділу двох однорідних прозорих середовищ з показниками заломлення
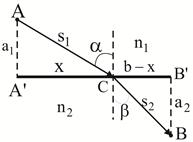
. Одержимо за допомогою принципу Ферма закон заломлення світла на границі розділу двох однорідних прозорих середовищ з показниками заломлення 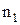 і
і 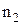 . Для цього знайдемо точку С, у якій повинний заломитися промінь, поширюючи від точки А до точки В, щоб оптична довжина шляху L була мінімальною. Нехай відрізок А'В'=b. Із малюнку свідчить:
. Для цього знайдемо точку С, у якій повинний заломитися промінь, поширюючи від точки А до точки В, щоб оптична довжина шляху L була мінімальною. Нехай відрізок А'В'=b. Із малюнку свідчить:
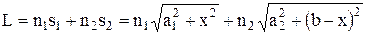 . (1)
. (1)
За умовою екстремуму: 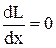 . Продиференціюємо вираз (1) за х і дорівняємо похідну нулеві:
. Продиференціюємо вираз (1) за х і дорівняємо похідну нулеві: 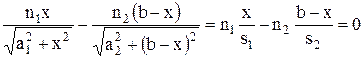 . Множники при
. Множники при 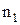 і
і 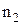 дорівнюють відповідно
дорівнюють відповідно 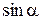 і
і 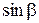 . Таким чином, одержуємо:
. Таким чином, одержуємо:  , що і повинно було довести.
, що і повинно було довести.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 540; Нарушение авторских прав?; Мы поможем в написании вашей работы!