
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Штучні способи здійснення інтерференції світла
|
|
|
|
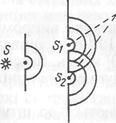
1. Спосіб Юнга. У 1807 р. Т. Юнг дістав два когерентні джерела світла у вигляді двох невеличких отворів в екрані, освітлюваному вузьким пучком світла. За принципом Гюйгенса–Френеля отвори  і
і 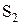 можна вважати вторинними когерентними джерелами світла, утворюваними джерелом S.
можна вважати вторинними когерентними джерелами світла, утворюваними джерелом S.
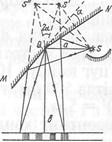
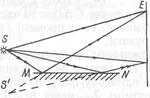
 2. Дзеркала Френеля. Френель здійснив інтерференцію світла в чистому вигляді за допомогою двох дзеркал, розміщених під кутом, близьким до 180°. За цим способом одна частина кожної світлової хвилі, випромінюваної точковим джерелом S, відбиваючись від дзеркала QN, а інша від дзеркала QМ, змінюють напрям поширення так, що далі збігаються на екрані та інтерферують. Щоб світло від джерела S безпосередньо не потрапляло на екран, джерело екранують.
2. Дзеркала Френеля. Френель здійснив інтерференцію світла в чистому вигляді за допомогою двох дзеркал, розміщених під кутом, близьким до 180°. За цим способом одна частина кожної світлової хвилі, випромінюваної точковим джерелом S, відбиваючись від дзеркала QN, а інша від дзеркала QМ, змінюють напрям поширення так, що далі збігаються на екрані та інтерферують. Щоб світло від джерела S безпосередньо не потрапляло на екран, джерело екранують.
 Когерентні хвилі, що утворюються способом відбиття від двох дзеркал, немовби випромінюються джерелами
Когерентні хвилі, що утворюються способом відбиття від двох дзеркал, немовби випромінюються джерелами 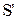 і
і 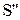 , які є уявними зображеннями в дзеркалах джерела S. Точки
, які є уявними зображеннями в дзеркалах джерела S. Точки 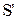 і
і 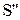 можна розглядати як два когерентних джерела світла, бо ж будь-яка зміна фази коливання в джерелі S тією самою мірою повторюватиметься в його зображеннях
можна розглядати як два когерентних джерела світла, бо ж будь-яка зміна фази коливання в джерелі S тією самою мірою повторюватиметься в його зображеннях 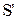 і
і 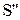 , але різниця фаз між ними залишатиметься сталою. Результат інтерференції світла в заданій точці на екрані залежатиме від різниці ходів хвиль від джерел
, але різниця фаз між ними залишатиметься сталою. Результат інтерференції світла в заданій точці на екрані залежатиме від різниці ходів хвиль від джерел 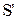 і
і 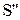 до даної точки. Очевидно, в тих точках інтерференційної картини на екрані, для яких різниця ходу хвиль дорівнює цілому числу довжин хвиль, будуть максимуми світла відповідної довжини хвилі; отже
до даної точки. Очевидно, в тих точках інтерференційної картини на екрані, для яких різниця ходу хвиль дорівнює цілому числу довжин хвиль, будуть максимуми світла відповідної довжини хвилі; отже 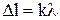 , де k = 0,1,2,… є умовою максимумів інтерференції світла. Якщо різниця ходу хвиль дорівнюватиме непарному числу півхвиль, то матимемо мінімуми інтенсивності світла:
, де k = 0,1,2,… є умовою максимумів інтерференції світла. Якщо різниця ходу хвиль дорівнюватиме непарному числу півхвиль, то матимемо мінімуми інтенсивності світла: 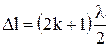 буде умовою мінімумів інтерференції світла. Виразимо умову максимумів інтерференції світла, враховуючи взаємне розміщення когерентних джерел, екрана та положення розглядуваної точки на екрані. Припустимо, що когерентні джерела
буде умовою мінімумів інтерференції світла. Виразимо умову максимумів інтерференції світла, враховуючи взаємне розміщення когерентних джерел, екрана та положення розглядуваної точки на екрані. Припустимо, що когерентні джерела 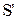 і
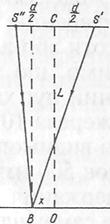
і 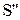 випромінюють монохроматичне світло з довжиною хвилі l. Нехай відстань між цими джерелами дорівнює d, а відстань від джерел до екрана L, причому d<<L. Зрозуміло, що в точці О на екрані, рівновіддаленій від джерел
випромінюють монохроматичне світло з довжиною хвилі l. Нехай відстань між цими джерелами дорівнює d, а відстань від джерел до екрана L, причому d<<L. Зрозуміло, що в точці О на екрані, рівновіддаленій від джерел 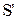 і
і 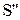 , матимемо максимум інтерференції світла. Сукупність таких точок на екрані визначить центральну смугу максимуму інтерференції світла. Нехай точка В на екрані належить до k–го максимуму інтерференції світла. Тоді за умовою максимумів:
, матимемо максимум інтерференції світла. Сукупність таких точок на екрані визначить центральну смугу максимуму інтерференції світла. Нехай точка В на екрані належить до k–го максимуму інтерференції світла. Тоді за умовою максимумів:  . Із прямокутних трикутників маємо:
. Із прямокутних трикутників маємо:
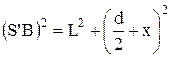 ,
, 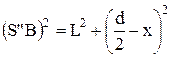 ,
,
Звідки: 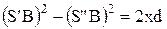 або
або 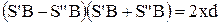 . Взявши до уваги, що
. Взявши до уваги, що 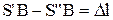 , а
, а 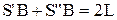 , дістанемо
, дістанемо 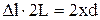 , звідки
, звідки 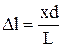 . Таким чином, максимуми інтерференції світла перебуватимуть від центрального максимуму на відстанях:
. Таким чином, максимуми інтерференції світла перебуватимуть від центрального максимуму на відстанях: 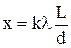 . Положення мінімумів знайдемо на відстанях:
. Положення мінімумів знайдемо на відстанях: 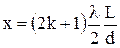 . Максимуми і мінімуми спостерігаються на екрані у вигляді світлих і темних смуг, паралельних одна одній. Неважко знайти, що відстань між двома сусідніми максимумами:
. Максимуми і мінімуми спостерігаються на екрані у вигляді світлих і темних смуг, паралельних одна одній. Неважко знайти, що відстань між двома сусідніми максимумами: 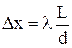 . З отриманого виразу випливає практична порада: максимуми добре розрізнятимуться, якщо відстань між джерелами світла буде якомога меншою.
. З отриманого виразу випливає практична порада: максимуми добре розрізнятимуться, якщо відстань між джерелами світла буде якомога меншою.
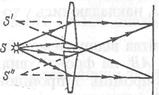 3. Біпризми Френеля. Аналогічно досліду з дзеркалами, Френель здійснив інтерференцію світла з двома призмами. Світлова хвиля, випромінювана джерелом S, за допомогою біпризм роздвоюється. Після заломлення в призмах світлові хвилі відхиляються в протилежних напрямах, тому перекриваються й інтерферують.
3. Біпризми Френеля. Аналогічно досліду з дзеркалами, Френель здійснив інтерференцію світла з двома призмами. Світлова хвиля, випромінювана джерелом S, за допомогою біпризм роздвоюється. Після заломлення в призмах світлові хвилі відхиляються в протилежних напрямах, тому перекриваються й інтерферують.
4. Дзеркало Ллойда. У схемі Ллойда частина світлової хвилі від джерела S безпосередньо потрапляє на екран Е, а інша – після відбивання від плоского дзеркала МN. На екрані обидві частини хвилі накладаються й інтерферують.
Інтерференція світла при відбиванні від прозорих пластинок і плівок.
Світлова хвиля, попадаючи на поверхню прозорого середовища, частково відбивається, а частково проходить у прозоре середовище, зазнаючи заломлення. Далі таке роздвоєння світлової хвилі відбудеться на протилежній поверхні прозорого середовища і т. д. Явища відбивання і заломлення світла в тонких прозорих пластинках і плівках супроводяться інтерференцією світла. Розглянемо інтерференцію світла від прозорої плоскопаралельної пластинки, товщиною d і показником заломлення n > 1. Нехай з повітря на пластинку падає пучок паралельних променів під кутом i. Промінь 1 у точці А частково відіб'ється, а частково пройде в пластинку під кутом г. Дійшовши до протилежної поверхні, в точці О він частково вийде за межі пластинки, а частково відіб'ється в напрямі ОС. У точці С частина променя 1 вийде в повітря під кутом i. Але в точку С падає та частково відбивається під тим самим кутом і промінь 2. Тому промені 1 і 2, накладаючись у точці С, будуть інтерферувати. 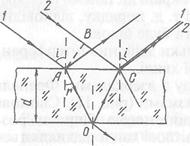 Для визначення результату інтерференції світла відшукаємо різницю ходів променів. Проведемо фронт хвилі АВ. На фронті хвилі обидва промені мали однакову фазу, а потім промінь 1 пройшов шлях (АО + ОС), а промінь 2 – шлях ВС. Для визначення різниці фаз треба ще врахувати, що шлях (АО + ОС) хвиля проходить всередині пластинки, а шлях ВС – в повітрі. Крім того, як показує дослід і теорія, промінь ВС, відбиваючись в точці С від оптично густішого середовища, змінює фазу на протилежну, що еквівалентно зміні його шляху на півхвилі. Врахувавши все сказане, можна записати:
Для визначення результату інтерференції світла відшукаємо різницю ходів променів. Проведемо фронт хвилі АВ. На фронті хвилі обидва промені мали однакову фазу, а потім промінь 1 пройшов шлях (АО + ОС), а промінь 2 – шлях ВС. Для визначення різниці фаз треба ще врахувати, що шлях (АО + ОС) хвиля проходить всередині пластинки, а шлях ВС – в повітрі. Крім того, як показує дослід і теорія, промінь ВС, відбиваючись в точці С від оптично густішого середовища, змінює фазу на протилежну, що еквівалентно зміні його шляху на півхвилі. Врахувавши все сказане, можна записати:
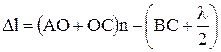 .
.
Виразимо останню рівність через товщину пластинки та кут падіння. Із малюнку випливає: 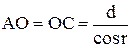 ,
, 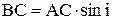 ,
, 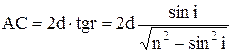 . У відповідності до закону заломлення
. У відповідності до закону заломлення 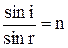 , відкіля
, відкіля 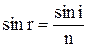 і
і 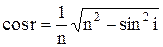 . Підставивши знайдені вирази в рівність різниці ходу і здійснивши деякі перетворення, маємо:
. Підставивши знайдені вирази в рівність різниці ходу і здійснивши деякі перетворення, маємо:  . Умова максимуму буде виконуватися, якщо
. Умова максимуму буде виконуватися, якщо 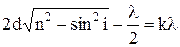 . Якщо
. Якщо 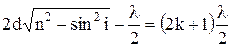 , буде спостерігатися мінімум інтерференції. В результаті інтерференції на пластинці утворяться кольорові смуги, які позначатимуть місця однакової товщини пластинки або плівки; їх називають смугами однакової товщини. Такі кольорові смуги можна спостерігати на дорогах після дощу, де розлите мастило чи пальне, на плоскій мильній плівці тощо.
, буде спостерігатися мінімум інтерференції. В результаті інтерференції на пластинці утворяться кольорові смуги, які позначатимуть місця однакової товщини пластинки або плівки; їх називають смугами однакової товщини. Такі кольорові смуги можна спостерігати на дорогах після дощу, де розлите мастило чи пальне, на плоскій мильній плівці тощо.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1526; Нарушение авторских прав?; Мы поможем в написании вашей работы!