Розрахунок гнучких ниток

Прикладной уровень

На прикладном уровне работает большинство сетевых приложений.

Эти программы имеют свои собственные протоколы обмена информацией, например, HTTP для WWW, FTP (передача файлов), SMTP (электронная почта), SSH (безопасное соединение с удалённой машиной), DNS (преобразование символьных имён в IP-адреса) и многие другие.

В массе своей эти протоколы работают поверх TCP или UDP и привязаны к определённому порту, например:

• HTTP на TCP-порт 80 или 8080,
• FTP на TCP-порт 20 (для передачи данных) и 21 (для управляющих команд),
• SSH на TCP-порт 22,
• запросы DNS на порт UDP (реже TCP) 53,
• обновление маршрутов по протоколу RIP на UDP-порт 520.

Эти порты определены Агентством по выделению имен и уникальных параметров протоколов (IANA).

К этому уровню относятся: Echo, Finger, Gopher, HTTP, HTTPS, IMAP, IMAPS, IRC, NNTP, NTP, POP3, POPS, QOTD, RTSP, SNMP, SSH, Telnet, XDMCP.

В компьютерных сетях из стека сетевых протоколов транспортного уровня чаще всего используются протоколы TCP и UDP, а также другие протоколы, которые используют идентификацию структуры данных с представлением конечных точек (хостов) в виде числовой последовательности. Такие конечные точки называются портами и идентифицируются согласно номерам портов. Номера портов, используемые для конкретных специфических целей, выделяет и регистрирует IANA (Internet Assigned Numbers Authority).

Основные протоколы TCP/IP по уровням модели OSI

Прикладной

BGP • HTTP • HTTPS • DHCP • IRC • SNMP • DNS • DNSSEC • NNTP • XMPP • SIP • BitTorrent • IPP • NTP • SNTP

Электронная почта	SMTP • POP3 • IMAP4
Передача файлов	FTP • TFTP • SFTP
Удалённый доступ	rlogin • Telnet • RDP

Представления

XDR • SSL

Сеансовый

ADSP • H.245 • iSNS • NetBIOS • PAP • RPC • L2TP • PPTP • RTCP • SMPP • SCP • SSH • ZIP • SDP

Транспортный

TCP • UDP • SCTP • DCCP • RUDP • RTP

Сетевой

IPv4 • IPv6 • IPsec • ICMP • IGMP • ARP • RARP • RIP2 • OSPF

Канальный

Ethernet • PPPoE • PPP • L2F • 802.11 Wi-Fi • 802.16 WiMax • Token ring • ARCNET • FDDI • HDLC • SLIP • ATM • DTM • X.25 • Frame relay • SMDS • STP

Физический

Ethernet • RS-232 • EIA-422 • RS-449 • RS-485

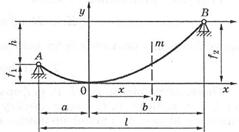
У техніці і будівництві (канатні дороги, висячі мости, електричні мережі, ланцюгові і пасові передачі, різні троси) трапляється ще один вид розтягнутих конструкцій — гнучкі нитки. Вони працюють тільки на розтяг і не чинять опору іншим видам деформації (рис. 4). Нехай ця гнучка нитка навантажена власною вагою і закріплена у двох точках на різних рівнях. Рис. 4

Горизон­тальну проекцію 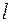між опо­рами називають прогином.

Вважаємо, що вага рівномі­рно розподілена по довжині його проекції на горизон­тальну вісь. Нехай інтенсив­ність q рівномірно розподі­лена по прогину. Це наван­таження (сила — довжина) може бути не тільки власною вагою, а й вагою льоду, тиску вітру та ін. Початок координат візьмемо у най­нижчій точці провисання. Виріжемо частину проводу x двома пере­різами (рис. 5). Сили 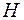і 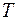в перерізах спрямовані по дотичній до кривої, оскільки нитка працює лише на розтяг. Складемо рівняння рівноваги вирізаного елемента – сума моментів усіх сил відносно точки прикладання сил T має вигляд

,

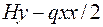звідки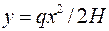

Це крива провисання точ­ки, отже, вона є параболою.

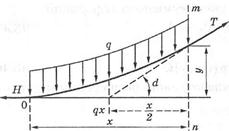Якщо обидві точки за­кріплення знаходяться на одному рівні, то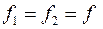. Величину 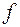називають стрілою провисання. При цьому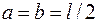, , 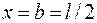, 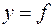тоді за формулою 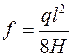. Рис.5

Звідси горизонтальна сила натягу нитки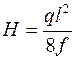

Із другого рівняння рівноваги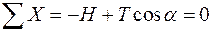

знаходимо силу розтягу в будь-якій точці: Рис. 5

.

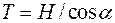Отже, якщо відом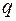і і 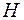, то із формули знайдемо провисан­ня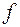, а за відомих 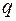, 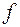– силу натягу 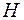. Зв'язок цих величин з дов­жиною 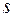нитки по кривій провисання установлюють за допомогою відомих формул аналітичної геометрії

.

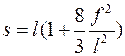Елемент довжини кривої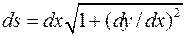. Із формул виходить, що .

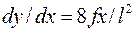Згідно з формулою, за малого провисання нитки кут 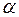ма­лий, тому можна вважати що зусилля в нитці є сталим і дорівнює 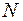. За цією величиною і розраховують міцність:

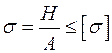
Врахувавши значення 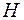, знайдемо

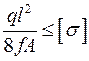звідки визначимо стрілу провисання.

Якщо брати до уваги тільки власну вагу нитки, 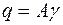, де 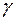– вага одиниці об'єму матеріалу, то .

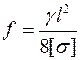Якщо точки закріплення нитки знаходяться на різних рівнях, то, підставивши в рівняння 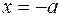? 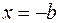, знайдемо :

; .

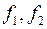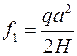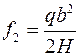Із другого рівняння

.

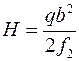Розділивши перше рівняння на друге, одержимо

.

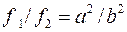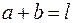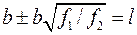Оскільки , то, або

.

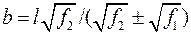Підставивши цей вираз у рівняння), отримаємо

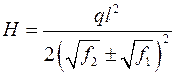
Наявність двох знаків означає, що можливі дві основні форми провисання нитки. Знак «мінус» беремо тоді, коли найнижча точка кривої провисання лежить у межах просвіту, а знак «плюс» — якщо найнижча точка поза прогоном.

Істотно впливають на міцність нитки і форму її провисання зміна температури та інтенсивність навантаження.

Іноді від міцності гнучких ниток (лінії електропередач, висячі мо­сти) повністю залежить міцність усієї конструкції. До 1973 p. найдов­шим висячим мостом вважали міст, побудований в 1964 p. у Нью- Йорку. Довжина його центральної частини 1298 м. У 1973 p. у Вели­кій Британії було споруджено міст через p. Хамбер з центральним прогоном завдовжки 1410 м і масою 27 тис. т. Цей підвісний міст тримається на двох тросах, які сплетені з 14 948 окремих дротинок.

3. Розрахунок тонкостінних посудин (оболонок)

Розрахункова схема тонкостінної посудини (оболонки, товщина якої значно менша порівняно з її габаритами) охоплює розрахунок багатьох інженерних конструкцій (котлів, баків, резервуарів, газо­вих, парових та водопровідних систем, гідро- і пневмоприводів), бу­дівельних споруд (куполів, перекриттів, башт), а також кровоносних судин і клітинних оболонок деяких рослин.

Загальна схема про рівновагу тонкостінної оболонки дуже склад­на в математичному відношенні і є предметом спеціального дослі­дження (існують школи з теорії і методів розрахунку оболонок (Київ, Харків, Дніпропетровськ, Москва, Казань). Цей матеріал викладено в багатьох підручниках і монографіях.

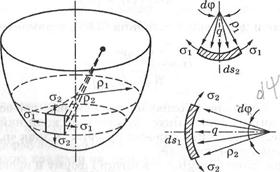
Розглянемо найважливіший для практики випадок, коли обо­лонка має форму поверхні обертання. Навантаження симетричні відносно осі обертання, а напруження, що виникають в оболонці, є сталими за товщиною.

Рис. 6

Отже, згин оболонки відсутній. Теорію обо­лонок, побудовану на цих припущеннях, називають безмоментною, або мембранною.

Нехай посудина, яка має форму тіла обертання з віссю (рис. 6), наповнена сипким тілом, рідиною або газом під тиском . Тиск газу рівномірно розподілений по поверхні оболонки. Тиск же рідини чи сипкого тіла змінюється залежно від вертикальної коор­динати, а в усіх точках горизонтального перерізу — сталий. Якщо тиск рівномірний, товщина посудини 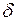дуже мала, то стінки посу­дини зазнаватимуть тільки розтягу або стиску.

Зі стінки оболонки виділимо нескінченно малий елемент двома площинами вздовж меридіанів і вздовж паралелей. Через те що тиск і оболонки симетричні, по площинах виділеного елемента не буде дотичних напружень, тобто вони будуть головними, по яких діятимуть головні напруження 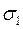і 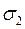. Нехай розміри сторін елемен­та – 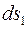і 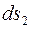, радіуси кривизни меридіана та паралел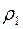і – і 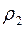, центральні кути – відповідно 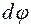і 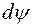(рис. 6), відповідні зусилля по гранях –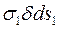і 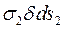. Ці зусилля зрівноважуються рівнодійною тиску, що виникає на внутрішній поверхні елемента: .

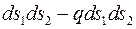Склавши рівняння рівноваги (суми проекцій усіх прикладених сил на нормаль до поверхні), одержимо

.

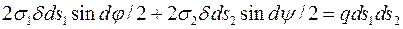Оскільки кути 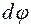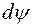нескінченно малі, то

;

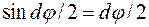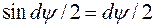
Тоді вираз запишемо так:

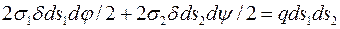
Врахувавши попередні рівності і те, що

;

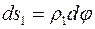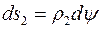
рівність запишемо так:

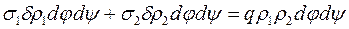
Після елементарних перетворень одержимо рівняння тонкостін­них посудин, так зване рівняння Лапласа:

.

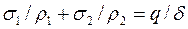Для сферичної посудини (оболонки) 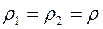; 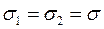. Тоді з рівняння отримаємо

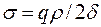
де 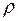– радіус сфери.

Для циліндричної оболонки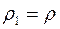, , 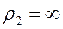тоді з рівняння за умови 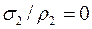напруження у поперечному напрямку

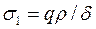
Напруження, що діють по твірній циліндричної оболонки, ви­значають з умови рівноваги по перерізу, перпендикулярному до осі циліндра:

,

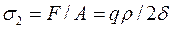де 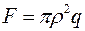– сила, що діє на днище циліндра; 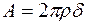– площа перерізу циліндра.

Із попередніх формул випливає, що напруження у поздовж­ньому перерізі вдвічі більше, ніж у поперечному. Тому умова міцно­сті для циліндричної оболонки має вигляд

.

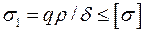Звідки, наприклад, товщина стінки для діючого тиску

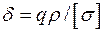
Дата добавления: 2014-01-07