Теорії міцності

Потенціальна енергія деформації

– загальна питома потенціальна енергія при об'ємному напруженому стані

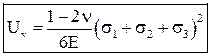– питома потенціальна енергія деформування, що йде на зміну об’єму.

– питома потенціальна енергія формозміни (витрачається на зміну форми елемента, який деформується).

Першочерговою задачею інженерного розрахунку є оцінка міцності деталі по відомому напруженому стані.

В практиці розрахунків на міцність існує п'ять основних критеріїв такої оцінки, або ж іншими словами – п'ять основних теорій міцності.

1. Теорія максимальних нормальних напружень: Міцність конструкції буде забезпечена в тому випадку, коли максимальні нормальні напруження, що виникають в її небезпечному перерізі (точці), не будуть перевищувати допустимі

(*)

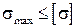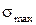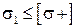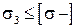За може виступати як , так і . І тоді: або , де

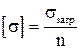, а під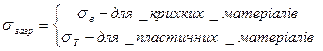

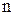–- коефіцієнт запасу міцності:

Недоліки:

Не враховуються два інших головних напруження. Ця теорія дає хороші результати тільки для дуже крихких матеріалів: стекло, фарфор, кераміка, цегла і їн.

2. Теорія максимальних відносних деформацій: міцність конструкції буде забезпечена в тому випадку, коли максимальні відносні лінійні деформації не будуть перевищувати допустимі деформацій.

(*)

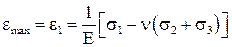– визначається при об'ємному напруженому

стані (О.Н.С.)

- визначається при лінійному напруженому стані.

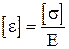. Підставимо значення деформації при лінійному напруженому стані (Л.Н.С.) в рівняння {*) будемо мати:

Þ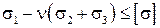

Еквівалентне напруження в цьому випадку:

Застосовується також тільки для крихких матеріалів.

3. Теорія максимальних дотичних напружень: міцність конструкції буде забезпечена в тому випадку, коли максимальні дотичні напруження, що виникають в її загрозливій (небезпечній) точці не будуть перевершувати допустимих дотичних напружень.

(*)

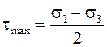– визначається при О.Н.С.

– визначається при Л.Н.С.

Підставляємо в рівняння (*) і маємо:

Þ

Ця теорія застосовується в основному для пластичних матеріалів. Її основний недолік:не враховується одне із головних нормальних напружень.

4. Енергетична теорія міцності: міцність конструкції буде забезпечена в тому випадку, коли питома потенційна енергія деформування матеріалу не перевищує величину допустимої енергії формозміни для нього.

(*)

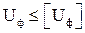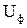визначається при О.Н.С. 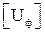визначається при Л.Н.С.

Таким чином, якщо питома потенційна енергія формозміни, що визначається при О.Н.С. буде дорівнювати:

А допустима питома потенційна енергія формозміни, що визначається при Л.Н.С. буде дорівнювати:

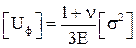, тоÞ

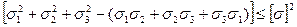
Для пластичних матеріалів:

або ж так:

чи так:

Для крихких матеріалів:

Еквівалентне напруження по цій теорії буде:

Використовуючи залежність для напружень на октаедричних площадках можемо записати, що: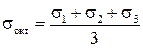

В розрахунках на міцність часто використовується так звана інтенсивність напружень, що зв'язана з 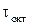залежністю: , або ж виразивши її через головні напруженнябудемо мати: Þ

Þ

Таким чином IV теорію міцності можна записати, виходячи із критерію постійності октаедричних напружень в такому вигляді:

Дата добавления: 2014-01-07