Полная горизонтальная дальность

Полная горизонтальная дальность есть абсцисса точки падения х_с (на рис. 5 х_с = ОС).

Для точки падения высота траектории у = 0. Следовательно, чтобы определить полную горизонтальную дальность полета снаряда, достаточно определить абсциссу той точки траектории, у которой ордината равна нулю, а абсцисса х не равна нулю.

Решая уравнение 1.1 для этих условий (х = х_с, у — 0), получим

.

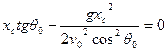Отсюда, полная горизонтальная дальность при стрельбе в безвоздушном пространстве равна

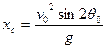. (1.2)

Анализ уравнения 1.2 приводит к следующим выводам.

1. Величина горизонтальной дальности при полете снаряда в безвоздушном пространстве зависит только от начальной скорости v ₀ и угла бросания θ₀.

2. Полная горизонтальная дальность при неизменном угле бросания возрастает пропорционально квадрату увеличения начальной скорости, например: при увеличении начальной скорости в два раза дальность полета возрастает в четыре раза, при увеличении начальной скорости снаряда в три раза дальность полета возрастает в девять раз и т. д.

3. При постоянной величине начальной скорости полная горизонтальная дальность зависит от угла бросания. Максимальная величина горизонтальной дальности будет достигнута, когда sin2θ₀=l, т. е. когда θ₀ = 45°.

Угол θ₀=45° называется углом наибольшей дальности для безвоздушного пространства.

4. Если стрелять с одинаковыми начальными скоростями при двух разных углах бросания, равноудаленных от угла наибольшей дальности, то полные горизонтальные дальности окажутся одинаковыми.

Траектории, отвечающие различным углам бросания, один из которых больше, а другой меньше 45°, и при которых получаются одинаковые дальности, называют сопряженными.

Сопряженных траекторий может быть бесчисленное множество. Некоторые из них для условий приводимого ниже примера показаны на рис. 6.

Пример. v₀ = 600 м/с, θ₀ равны 12°, 24°, 36°, 45°, 54°, 66°, 78°.

Приняв g = 10 м/с, получим:

θ0 град
хс км	14,652	26,748	34,236	36,000	34,236	26,748	14,652

Из данных таблицы следует, что сопряженными траекториями являются траектории, получаемые при углах бросания 12 и 78°, 24 и 66°, 36 и 54°.

Таким образом, одну и ту же цель, находящуюся в пределах досягаемости орудия, можно поразить при двух углах бросания, один из которых меньше, а другой больше 45°.

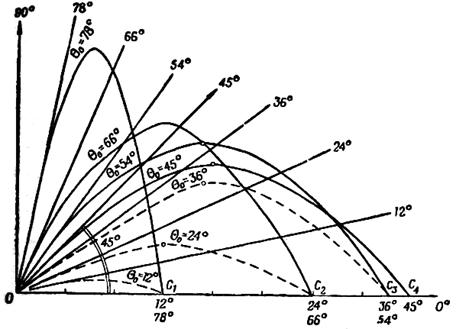
Рис. 6. Сопряженные траектории

Лекція 8

Тема 3. Заняття 3. Рух снаряда в безповітряному просторі

1. Висота траєкторії.

2. Швидкість польоту.

3. Час польоту.

Дата добавления: 2014-01-07